题目内容
【题目】已知函数f(x)=x2+bx+c,其图象与y轴的交点为(0,1),且满足f(1﹣x)=f(1+x).
(1)求f(x);
(2)设![]() ,m>0,求函数g(x)在[0,m]上的最大值;
,m>0,求函数g(x)在[0,m]上的最大值;
(3)设h(x)=lnf(x),若对于一切x∈[0,1],不等式h(x+1﹣t)<h(2x+2)恒成立,求实数t的取值范围.
【答案】(1)f(x)=x2﹣2x+1;(2)
(3)实数t的取值范围是﹣1<t<0.
【解析】试题分析:(1)根据截距和对称轴得出b,c的值,得出f(x)的解析式;
(2)作出g(x)的函数图象,根据图象得出结论;
(3)化简h(x)解析式,根据函数单调性得出关于t的恒等式,从而求出t的范围.
试题解析:
(1)∵图象与y轴的交点为(0,1),∴c=1,
∵f(1﹣x)=f(1+x),
∴函数f(x)的图象关于直线x=1对称,∴b=﹣2,
∴f(x)=x2﹣2x+1,
(2)∵f(x)=x2﹣2x+1=(x﹣1)2,
∴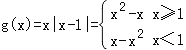 ,
,
作出g(x)的函数图象如图所示:

当0<m≤![]() 时,gmax(x)=g(m)=m﹣m2,
时,gmax(x)=g(m)=m﹣m2,
当![]() <m≤
<m≤![]() 时,gmax(x)=g(
时,gmax(x)=g(![]() )=
)=![]() ,
,
当m>![]() 时,gmax(x)=g(m)=m2﹣m,
时,gmax(x)=g(m)=m2﹣m,
综上, 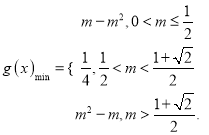 .
.
(3)h(x)=2ln|x﹣1|,
所以h(x+1﹣t)=2ln|x﹣t|,h(2x+2)=2ln|2x+1|,
当x∈[0,1]时,|2x+1|=2x+1,
所以不等式等价于0<|x﹣t|<2x+1恒成立,
解得﹣x﹣1<t<3x+1,且x≠t,
由x∈[0,1],得﹣x﹣1∈[﹣2,﹣1],3x+1∈[1,4],
所以﹣1<t<1,
又x≠t,∵t[0,1],
∴实数t的取值范围是﹣1<t<0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目