题目内容
【题目】已知函数![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(1)求f(x)的表达式和极值.
(2)若f(x)在区间[m,m+4]上是单调函数,试求m的取值范围.
【答案】(1)f(x)=2x3-3x2-12x+3,当x=-1时,有极大值10;当x=2时,有极小值-17(2)m≤-5或m≥2
【解析】试题分析:(1)由题意得![]() 和2为导函数两个零点,根据韦达定理可求
和2为导函数两个零点,根据韦达定理可求![]() ,列表分析导函数符号变化规律,确定极值,(2)由(1)可得函数单调区间,根据
,列表分析导函数符号变化规律,确定极值,(2)由(1)可得函数单调区间,根据![]() 为单调区间一个子集可得不等式
为单调区间一个子集可得不等式![]() 或
或![]() 或
或![]() ,解不等式可得
,解不等式可得![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 的两根为
的两根为![]() 和2,∴
和2,∴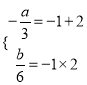 ,得
,得![]() ,
,
∴![]() ,∴
,∴![]() ,令
,令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,所以
,所以![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]() .
.
(2)由(1)知, ![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 或
或![]() 或
或![]() ,∴
,∴![]() 或
或![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目