题目内容
【题目】已知函数f(x)对一切x,y∈R都有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0.
(1)求f(0)的值;
(2)求f(x)的解析式;
(3)已知a∈R,设P:当 ![]() 时,不等式f(x)+3<2x+a恒成立,Q:当x∈[﹣2,2]时,g(x)=f(x)﹣ax是单调函数,如果记使P成立的实数a的取值的集合为A,使Q成立的实数a的取值的集合为B,求A∩RB.
时,不等式f(x)+3<2x+a恒成立,Q:当x∈[﹣2,2]时,g(x)=f(x)﹣ax是单调函数,如果记使P成立的实数a的取值的集合为A,使Q成立的实数a的取值的集合为B,求A∩RB.
【答案】
(1)解:∵f(x+y)﹣f(y)=x(x+2y+1),f(1)=0,取x=﹣1,y=1得f(0)﹣f(1)=﹣(﹣1+2+1),f(0)=﹣2
(2)解:取y=0,得f(x)﹣f(0)=x(x+1),故f(x)=x2+x﹣2
(3)解:(i)当 ![]() 时,不等式f(x)+3<2x+a恒成立,即x2﹣x+1<a恒成立
时,不等式f(x)+3<2x+a恒成立,即x2﹣x+1<a恒成立
记h(x)=x2﹣x+1,对称轴 ![]() ,h(x)max=h(0)=1,
,h(x)max=h(0)=1,
所以a>1,即A=(1,+∞)
(ii)g(x)=x2+(1﹣a)x﹣2,对称轴: ![]() ,
,
由于x∈[﹣2,2]时,g(x)是单调函数,所以 ![]()
即A=(﹣∞,﹣3]∪[5,+∞),所以CRB=(﹣3,5),A∩CRB=(1,5)
【解析】(1)令x=﹣1,y=1,利用f(x+y)﹣f(y)=x(x+2y+1),即可求得f(0)的值;(2)令y=0,则f(x)﹣f(0)=x(x+1),结合f(0)=﹣2,可求f(x)的解析式;(3)不等式f(x)+3<2x+a,即x2+x﹣2+3<2x+a,即x2﹣x+1<a,从而可得A,根据g(x)在[﹣2,2]上是单调函数,可求B,从而可求A∩CRB.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】某同学在求函数y=lgx和 ![]() 的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )
的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )
x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
A.(2.125,2,25)
B.(2.75,2.875)
C.(2.625,2.75)
D.(2.5,2.625)
【题目】已知椭圆E: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且离心率e为
,且离心率e为 ![]() .
. 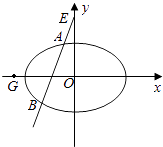
(1)求椭圆E的方程;
(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G ![]() 与以线段AB为直径的圆的位置关系,并说明理由.
与以线段AB为直径的圆的位置关系,并说明理由.
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]() ,其中
,其中![]() )
)