题目内容
(本小题满分12分)
设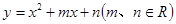 ,当
,当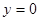 时,对应
时,对应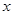 值的集合为
值的集合为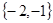 .
.
(1)求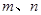 的值;(2)若
的值;(2)若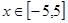 ,求该函数的最值.
,求该函数的最值.
设
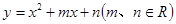 ,当
,当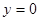 时,对应
时,对应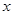 值的集合为
值的集合为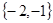 .
.(1)求
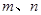 的值;(2)若
的值;(2)若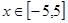 ,求该函数的最值.
,求该函数的最值.(1)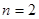 .(2)当
.(2)当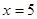 时,该函数取得最大值
时,该函数取得最大值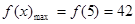
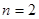 .(2)当
.(2)当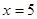 时,该函数取得最大值
时,该函数取得最大值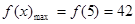
本试题主要是考查了二次函数的最值和二次函数的解析式的求解。
(1)因为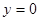 即
即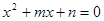 ,则
,则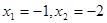 为其两根,
为其两根,
由韦达定理知: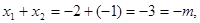 所以
所以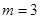 ,同理
,同理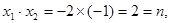 ,可知m,n的值。
,可知m,n的值。
(2)因为由(1)知: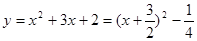 ,那个根据对称轴和定义域的关系而可知函数的最值。
,那个根据对称轴和定义域的关系而可知函数的最值。
解:(1)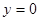 即
即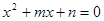 ,则
,则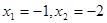 为其两根,
为其两根,
由韦达定理知: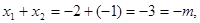 所以
所以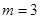 ,
,
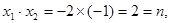 所以
所以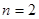 .
.
(2)由(1)知: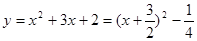 ,
,
因为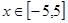 ,所以,当
,所以,当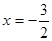 时,该函数取得最小值
时,该函数取得最小值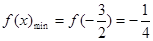 ,
,
又因为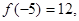
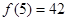 ,
,
所以当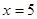 时,该函数取得最大值
时,该函数取得最大值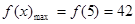
(1)因为
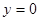 即
即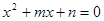 ,则
,则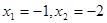 为其两根,
为其两根,由韦达定理知:
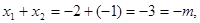 所以
所以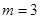 ,同理
,同理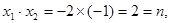 ,可知m,n的值。
,可知m,n的值。(2)因为由(1)知:
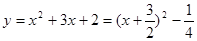 ,那个根据对称轴和定义域的关系而可知函数的最值。
,那个根据对称轴和定义域的关系而可知函数的最值。解:(1)
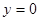 即
即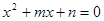 ,则
,则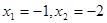 为其两根,
为其两根,由韦达定理知:
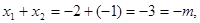 所以
所以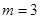 ,
, 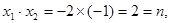 所以
所以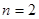 .
.(2)由(1)知:
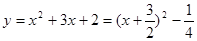 ,
,因为
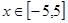 ,所以,当
,所以,当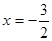 时,该函数取得最小值
时,该函数取得最小值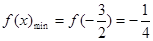 ,
,又因为
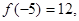
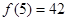 ,
,所以当
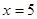 时,该函数取得最大值
时,该函数取得最大值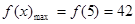

练习册系列答案
相关题目
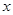 的方程
的方程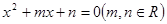 的一个根是
的一个根是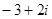 ,则
,则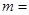 _________.
_________.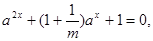 (a>0,且
(a>0,且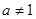 )有解,则m的取值范围是( )
)有解,则m的取值范围是( )

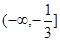
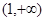
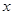 的二次函数
的二次函数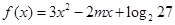 在区间
在区间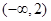 上是单调函数,则
上是单调函数,则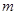 的取值范围是( )
的取值范围是( )



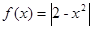 ,若
,若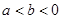 ,且
,且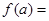
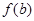 ,则
,则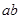 的取值范围是
的取值范围是 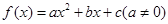 满足
满足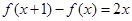 ,且
,且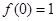 .(1)求
.(1)求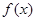 的解析式;(2)若在区间
的解析式;(2)若在区间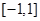 上,不等式
上,不等式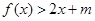 恒成立,求实数
恒成立,求实数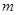 的取值范围.
的取值范围.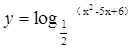 的单调增区间为( )
的单调增区间为( ) ,+∞)
,+∞)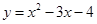 的定义域为
的定义域为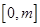 ,值域为
,值域为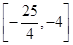 ,则
,则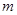 的取值集合为 .
的取值集合为 .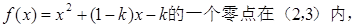 则实数k的取值范围是()
则实数k的取值范围是()