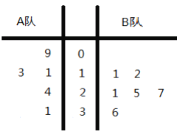
题目内容
【题目】已知函数f（x）=x2+|x﹣a|．
（1）当a=1时，求函数f（x）的最小值；
（2）试讨论函数f（x）的奇偶性，并说明理由．
【答案】（1）
；
（2）见解析．
【解析】
试题（1）将f（x）化简成分段函数，讨论f（x）的单调性，求出最小值；
（2）将f（x）化简成分段函数，对a进行讨论，得出结论．
解：（1）a=1时，f（x）=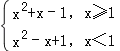
，
∴f（x）在（﹣∞，
）上是减函数，在[，1）上是增函数，在[1，+∞）上是增函数．
∴fmin（x）=f（
）=．
（2）f（x）=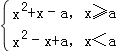
，
①若a＞0，当x≥a时，﹣x≤﹣a＜0，
f（x）=x2+x﹣a，f（﹣x）=x2+x+a，∴f（﹣x）≠±f（x）．
∴f（x）为非奇非偶函数．
②若a＜0，当x＜a时，﹣x＞﹣a＞0，
f（x）=x2﹣x+a，f（﹣x）=x2﹣x﹣a，∴f（﹣x）≠±f（x）．
∴f（x）为非奇非偶函数．
③若a=0，当x≥0时，f（x）=x2+x，f（﹣x）=x2+x，∴f（x）=f（﹣x），
当x＜0时，f（x）=x2﹣x，f（﹣x）=x2﹣x，∴f（x）=f（﹣x）．
∴f（x）是偶函数．
综上，当a=0时，f（x）是偶函数，
当a≠0时，f（x）为非奇非偶函数．
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动，治疗特种病的创新药研发成了当务之急．为此，某药企加大了研发投入，市场上治疗一类慢性病的特效药品
的研发费用
（百万元）和销量
（万盒）的统计数据如下：
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
（1）求与的相关系数
精确到0.01，并判断与的关系是否可用线性回归方程模型拟合？（规定：
时，可用线性回归方程模型拟合）；
（2）该药企准备生产药品的三类不同的剂型
，
，
，并对其进行两次检测，当第一次检测合格后，才能进行第二次检测．第一次检测时，三类剂型，，合格的概率分别为
，
，
，第二次检测时，三类剂型，，合格的概率分别为，，
．两次检测过程相互独立，设经过两次检测后，，三类剂型合格的种类数为
，求的数学期望．
附：（1）相关系数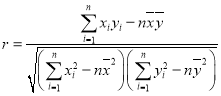
（2）
，
，
，
．
