题目内容
设定义域为R的函数f(x)满足下列条件:①对任意x∈R,f(x)+f(-x)=0;②对任意x∈[-1,1],都有![]() >0,且f(-1)=-1.若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是( )
>0,且f(-1)=-1.若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是( )
A.-2≤t≤2
B.t≤-![]() 或t=0或t≥
或t=0或t≥![]()
C.-![]() ≤t≤
≤t≤![]()
D.t≤-2或t=0或t≥2
D
[分析] 函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立⇔在[-1,1]上,f(x)max≤t2-2at+1,于是由函数的性质可以先求出f(x)max.
[解析] 由题知f(x)是奇函数,在[-1,1]上是增函数,且f(-1)=-1,所以在[-1,1]上,f(x)max=f(1)=-f(-1)=1.函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立⇔t2-2at+1≥1⇔t2-2at≥0恒成立.
设g(a)=t2-2at,a∈[-1,1],则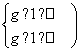 ⇔
⇔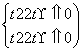 ⇔t≤-2或t=0或t≥2.故选D.
⇔t≤-2或t=0或t≥2.故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目