题目内容
【题目】如图,在平面直角坐标系xOy中,椭圆E:![]() 的离心率为
的离心率为![]() ,点A(2,1)是椭圆E上的点.
,点A(2,1)是椭圆E上的点.
(1)求椭圆E的方程;
(2)过点A作两条互相垂直的直线l1,l2分別与椭圆E交于B,C两点,己知△ABC的面积为![]() ,求直线BC的方程.
,求直线BC的方程.

【答案】(1)![]() (2)x=
(2)x=![]() 或x-4y-2=0
或x-4y-2=0
【解析】
(1)将点![]() 的坐标代入椭圆方程,结合
的坐标代入椭圆方程,结合![]() ,解方程组求得
,解方程组求得![]() 的值,从而得到椭圆方程.(2)首先考虑直线
的值,从而得到椭圆方程.(2)首先考虑直线![]() 斜率不存在的情况,此时面积不合题意.当直线
斜率不存在的情况,此时面积不合题意.当直线![]() 斜率存在是,设出之心方程,联立直线方程和椭圆方程,用弦长公式求出
斜率存在是,设出之心方程,联立直线方程和椭圆方程,用弦长公式求出![]() ,同理求得
,同理求得![]() ,再用三角形面积为
,再用三角形面积为![]() 列方程,求得直线的斜率,由此求得
列方程,求得直线的斜率,由此求得![]() 的坐标,进而求得直线
的坐标,进而求得直线![]() 的方程.
的方程.
解:(1) 因为椭圆E的离心率为![]() ,所以
,所以![]() =
=![]() ,
,
又因为a2=b2+c2=2c2,所以a2=2b2=2c2,
因为点A(2,1)是椭圆E上的点,所以![]() +
+![]() =1
=1
解得b2=3,a2=6,
所以椭圆E的标准方程是![]() +
+![]() =1.
=1.
(2)当AB的斜率不存在或为0时,AB=4或2,此时△ABC的面积为4,不合题意舍去;
当AB的斜率存在且不为0时,设AB的斜率为k,则直线AB方程为y-1=k(x-2),
由 解得
解得![]() 或
或
AB=![]() |
|![]() -2|=
-2|=![]() |
|![]() |,
|,
同理将上式中的k用-![]() 替换,得AC=
替换,得AC=![]() |
|![]() |,
|,
因为△ABC的面积为![]() ,所以
,所以![]() AB AC=
AB AC=![]()
![]() |
|![]() |
|![]() |
|![]() |=
|=![]() ,
,
化简得![]() =
=![]() ,
,
当k2≥1时,原方程可化为8k4-25k2-28=0,解得k2=4,
当k2≤1时,解得k2=![]() ,
,
即k=2或-2或![]() 或-
或-![]() ,
,
当AB的斜率2时,AC的斜率-![]() ,此时B点坐标(
,此时B点坐标(![]() ,-
,-![]() ),C点坐标(
),C点坐标(![]() ,
,![]() ),
),
此时直线BC的方程为x=![]() ,
,
当AB的斜率-2时,AC的斜率![]() ,此时B点坐标(
,此时B点坐标(![]() ,
,![]() ),C点坐标(-2,-1),
),C点坐标(-2,-1),
此时直线BC的方程为x-4y-2=0,
综上,直线BC的方程为x=![]() 或x-4y-2=0.
或x-4y-2=0.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】已知从甲地到乙地的公路里程约为240(单位:km).某汽车每小时耗油量Q(单位:L)与速度x(单位:![]() )(
)(![]() )的关系近似符合以下两种函数模型中的一种(假定速度大小恒定):①
)的关系近似符合以下两种函数模型中的一种(假定速度大小恒定):①![]() ,②
,②![]() ,经多次检验得到以下一组数据:
,经多次检验得到以下一组数据:
x | 0 | 40 | 60 | 120 |
Q | 0 |
|
| 20 |
(1)你认为哪一个是符合实际的函数模型,请说明理由;
(2)从甲地到乙地,这辆车应以多少速度行驶才能使总耗油量最少?
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩![]() 、物理成绩
、物理成绩![]() 进行分析.下面是该生7次考试的成绩.
进行分析.下面是该生7次考试的成绩.
数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的证明;
(2)已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
是线性相关的,若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?并请你根据物理成绩与数学成绩的相关性,给出该生在学习数学、物理上的合理建议.
参考公式:方差公式:![]() ,其中
,其中![]() 为样本平均数.
为样本平均数. ,
,![]() 。
。
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每本单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于的线性回归方程;
(2)若该书每本的成本为![]() 元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: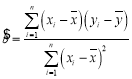
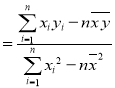 ,
,![]() .
.

