题目内容

13．讨论f（x）=ex-ln（x+1）的单调性．

分析 先求导，再令导数等于0，再判断导数大于0时和导数小于0时，x的范围，继而得到函数的单调性．

解答 解：∵f（x）=ex-ln（x+1），
∴f′（x）=ex-$\frac{1}{x+1}$=$\frac{（x+1）{e}^{x}-1}{x+1}$，x＞-1，
令f′（x）=0，解得x=0，
当f′（x）＞0时，即x＞0时，函数单调递增，
当f′（x）＜0时，即-1＜x＜0时，函数单调递减，
∴函数f（x）在（-1，0）上单调递减，在（0，+∞）上单调递增．

点评 本题考查了导数和函数的单调性的关系，属于基础题．

练习册系列答案
相关题目
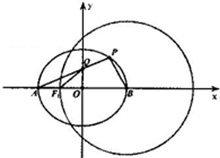3．如图，点A，B分别是椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，圆B：（x-2）2+y2=9，经过椭圆E的左焦点F．
（Ⅰ）求椭圆E的方程；
（Ⅱ）过A作直线l与y轴交于点Q，与椭圆E交于点P（异于A）．求$\overrightarrow{{F_1}Q}$•$\overrightarrow{BP}$的取值范围．
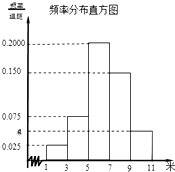4．为了解某校今年高一年级女生的身体素质状况，从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试，成绩低于5米为不合格，成绩在5至7米（含5米不含7米）的为及格，成绩在7米至11米（含7米和11米，假定该校高一女生掷铅球均不超过11米）为优秀．把获得的所有数据，分成[1，3），[3，5），[5，7），[7，9），[9，11]五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
（1）求实数a的值；
（2）参加“掷铅球”项目测试的人数．
1．设i为虚数单位，则1+i+i2+i3+…+i10=i．
8．已知下列命题：①命题“?x∈R，2x2+1＞5x”的否定是“?x∈R，2x2+1＜5x”；
②已知p，q为两个命题，若“p∨q”为假命题，则“（￢p）∧（￢q）”为真命题；
③“a＞2”是“a＞5”的充分不必要条件；
④“若xy=0，则x=0且y=0”的逆否命题为真命题．
其中所有真命题的序号是②．
18．已知定义在[-1.1]上的函数f（x）=-2|x|+1，设f1（x）=f（x），fn+1（x）=f[fn（x）]，n∈N*，若关于x的方程f3（x）-mx+m=0有5个实数根，则实数m的取值范围是$（{\frac{2}{3}，1}）∪\left\{{-\frac{4}{5}}\right\}$．
5．设函数h（x）=$\frac{1}{2}a{x^2}$+2ax（a∈R），g（x）=lnx．
（1）若f（x）=h（x）-3g（x）在x=1处有极值，求a；
（2）若f（x）在[2，3]上为增函数，求a的取值范围；
（3）证明：?x∈（0，+∞），$\frac{x-1}{x}$≤g（x）≤x-1．
2．关于函数$f（x）={sin^2}x-{（\frac{2}{3}）^{|x|}}+\frac{1}{2}$，有下面四个结论：
①f（x）是偶函数；      
②无论x取何值时，f（x）＜$\frac{1}{2}$恒成立；
③f（x）的最大值是$\frac{3}{2}$；  
④f（x）的最小值是-$\frac{1}{2}$．
其中正确的结论是①④．
3．设函数f（x）在x=x0处有导数，且$\underset{lim}{△x→0}$$\frac{f（{x}_{0}+2△x）-f（{x}_{0}）}{△x}$=1，则f′（x0）=（　　）
A．1B．0C．2D．$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网