题目内容
(1)求与向量a=(2,-1,2)共线且满足方程a·x=-18的向量x的坐标;
(2)已知A、B、C三点坐标分别为(2,-1,2),(4,5,-1),(-2,2,3),求点P的坐标使得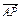 =
=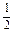 (
(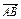 -
-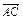 );
);
(3)已知a=(3,5,-4),b=(2,1,8),求:①a·b;②a与b夹角的余弦值;
③确定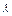 ,
,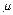 的值使得
的值使得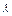 a+
a+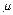 b与z轴垂直,且(
b与z轴垂直,且(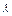 a+
a+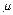 b)·(a+b)=53.
b)·(a+b)=53.
(2)已知A、B、C三点坐标分别为(2,-1,2),(4,5,-1),(-2,2,3),求点P的坐标使得
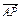 =
=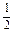 (
(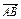 -
-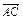 );
);(3)已知a=(3,5,-4),b=(2,1,8),求:①a·b;②a与b夹角的余弦值;
③确定
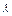 ,
,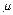 的值使得
的值使得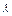 a+
a+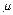 b与z轴垂直,且(
b与z轴垂直,且(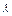 a+
a+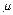 b)·(a+b)=53.
b)·(a+b)=53.(1)(-4,2,-4)(2)P点坐标为(5,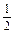 ,0)(3)
,0)(3)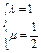
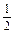 ,0)(3)
,0)(3)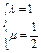
(1)∵x与a共线,故可设x=ka,
由a·x=-18得a·ka=k|a|2=k(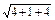 )2=9k,
)2=9k,
∴9k=-18,故k=-2.
∴x=-2a=(-4,2,-4).
(2)设P(x,y,z),则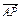 =(x-2,y+1,z-2),
=(x-2,y+1,z-2),
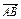 =(2,6,-3),
=(2,6,-3),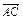 =(-4,3,1),
=(-4,3,1),
∵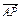 =
=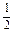 (
(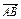 -
-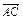 ).
).
∴(x-2,y+1,z-2)=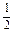 [(2,6,-3)-(-4,3,1)]
[(2,6,-3)-(-4,3,1)]
=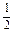 (6,3,-4)=(3,
(6,3,-4)=(3, ,-2)
,-2)
∴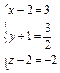 ,解得
,解得
∴P点坐标为(5,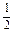 ,0).
,0).
(3)①a·b=(3,5,-4)·(2,1,8)
=3×2+5×1-4×8=-21.
②∵|a|=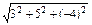 =5
=5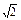 ,
,
|b|= =
=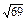 ,
,
∴cos〈a,b〉=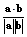 =
=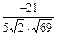 =-
=-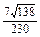 .
.
∴a与b夹角的余弦值为-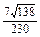 .
.
③取z轴上的单位向量n=(0,0,1),a+b=(5,6,4).
依题意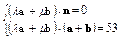
即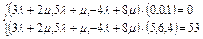
故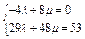 解得
解得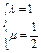 .
.
由a·x=-18得a·ka=k|a|2=k(
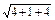 )2=9k,
)2=9k,∴9k=-18,故k=-2.
∴x=-2a=(-4,2,-4).
(2)设P(x,y,z),则
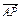 =(x-2,y+1,z-2),
=(x-2,y+1,z-2),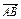 =(2,6,-3),
=(2,6,-3),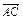 =(-4,3,1),
=(-4,3,1),∵
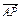 =
=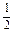 (
(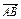 -
-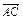 ).
).∴(x-2,y+1,z-2)=
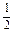 [(2,6,-3)-(-4,3,1)]
[(2,6,-3)-(-4,3,1)]=
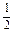 (6,3,-4)=(3,
(6,3,-4)=(3, ,-2)
,-2)∴
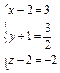 ,解得
,解得
∴P点坐标为(5,
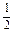 ,0).
,0).(3)①a·b=(3,5,-4)·(2,1,8)
=3×2+5×1-4×8=-21.
②∵|a|=
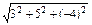 =5
=5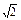 ,
,|b|=
 =
=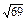 ,
,∴cos〈a,b〉=
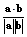 =
=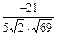 =-
=-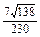 .
.∴a与b夹角的余弦值为-
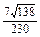 .
.③取z轴上的单位向量n=(0,0,1),a+b=(5,6,4).
依题意
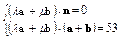
即
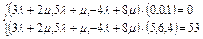
故
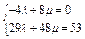 解得
解得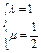 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
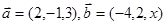 ,若
,若
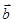 则
则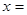 ______。
______。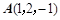 关于面
关于面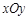 的对称点为
的对称点为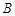 ,而
,而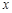 轴的对称点为
轴的对称点为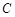 ,则
,则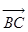 = ( )
= ( )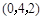
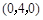
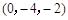
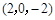
 ,
,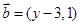 (
(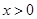 ,
, ),若
),若 ∥
∥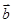 ,则
,则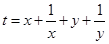 的最小
的最小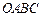 中,
中,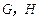 分别是
分别是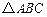 ,
,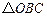 的重心,设
的重心,设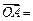
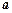 ,
,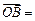
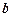 ,
,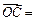
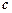 ,试用向量
,试用向量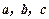 表示向量
表示向量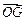 和
和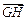 .
. ,
,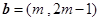 .若向量
.若向量 与
与 共线,则实数
共线,则实数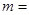 _______.
_______.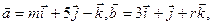 若
若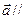
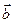 则实数
则实数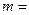 ______,
______, _______。
_______。 、
、 ,则该球的半径R及点A、B在该球面上的最短距离
,则该球的半径R及点A、B在该球面上的最短距离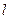 分别为
分别为 B.
B.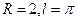 C.
C. D.
D.