题目内容
【题目】已知函数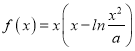
，关于x的方程f（x）＝a存在四个不同实数根，则实数a的取值范围是（ ）
A.（0，1）∪（1，e）B.
C.
D.（0，1）
【答案】D
【解析】
原问题转化为
有四个不同的实根，换元处理令t
，对g（t）
进行零点个数讨论.
由题意，a＞0，令t，
则f（x）＝a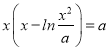
．
记g（t）．
当t＜0时，g（t）＝2ln（﹣t）
（t
）单调递减，且g（﹣1）＝0，
又g（1）＝0，∴只需g（t）＝0在（0，+∞）上有两个不等于1的不等根．
则
，
记h（t）
（t＞0且t≠1），
则h′（t）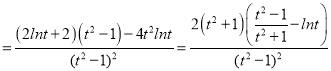
．
令φ（t）
，则φ′（t）
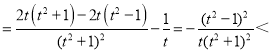0．
∵φ（1）＝0，∴φ（t）在（0，1）大于0，在（1，+∞）上小于0．
∴h′（t）在（0，1）上大于0，在（1，+∞）上小于0，
则h（t）在（0，1）上单调递增，在（1，+∞）上单调递减．
由
，可得
，即a＜1．
∴实数a的取值范围是（0，1）．
故选：D．
练习册系列答案
相关题目
