题目内容
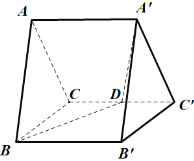
【题目】如图,在四棱锥![]() 中,
中,![]() 为等边三角形,边长为2,
为等边三角形,边长为2,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面ABCD.
平面ABCD.
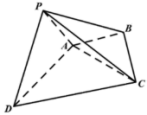
(1)证明:![]() 平面PAD;
平面PAD;
(2)求平面PAD与平面PBC所成锐二面角的余弦值;
(3)棱PD上是否存在一点E,使得![]() 平面PBC?若存在,求出
平面PBC?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)棱PD上存在一点E,使得
;(3)棱PD上存在一点E,使得![]() 平面PBC,且
平面PBC,且![]() .
.
【解析】
(1)用面面垂直的性质定理证明线面垂直;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,得
,得![]() 平面
平面![]() ,以
,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系,用平面的法向量的夹角求二面角;
轴,建立如图所示的空间直角坐标系,用平面的法向量的夹角求二面角;
(3)假设棱PD上存在一点E,使得![]() 平面PBC,设
平面PBC,设![]() ,由
,由![]() 与平面
与平面![]() 的法向量垂直求得
的法向量垂直求得![]() ,如果求不出,说明不存在.
,如果求不出,说明不存在.
(1)∵平面![]() 平面ABCD,
平面ABCD,![]() ,平面
,平面![]() 平面ABCD
平面ABCD![]() ,
,![]() 平面ABCD,∴
平面ABCD,∴![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由于
,由于![]() 是等边三角形,所以
是等边三角形,所以![]() ,由平面
,由平面![]() 平面ABCD,得
平面ABCD,得![]() 平面
平面![]() ,
,![]() ,
,
以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,

![]() ,
,![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则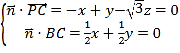 ,取
,取![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
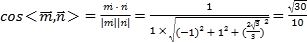 ,
,
∴平面PAD与平面PBC所成锐二面角的余弦值为![]() ;
;
(3)假设棱PD上存在一点E,使得![]() 平面PBC,设
平面PBC,设![]()
![]() ,
,
由(2)![]() ,
,![]() ,
,
![]() ,又平面
,又平面![]() 的一个法向量是
的一个法向量是![]() ,
,
∴![]() ,解得
,解得![]() ,∴
,∴![]() .
.
∴棱PD上存在一点E,使得![]() 平面PBC,且
平面PBC,且![]() .
.

【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
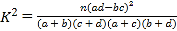 (其中
(其中![]() ).
).