Question

抛物线y=x²（-2≤x≤2）绕y轴旋转一周形成一个如图所示的旋转体，在此旋转体内水平放入一个正方体，使正方体的一个面恰好与旋转体的开口面平齐，则此正方体的体积是______．

Answer 1

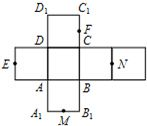
作过正方体的两条相对侧棱的截面图如图，
设正方体AC₁的棱长AA₁=a，则底面对角线AC=

2

a，
∴A点的横坐标等于

2

2

a，
结合抛物线方程可得A点纵坐标：y=(

2

2

a)2=

1

2

a2，
根据题意可知A点纵坐标为4-a．
∴

1

2

a2=4-a，解得a=2，
因此正方体的棱长是2，体积积V=2³=8．
故答案为：8