题目内容
已知正三棱锥的高为1,底面边长为2
,其内有一个球和该三棱锥的四个面都相切,求:
(1)棱锥的全面积;
(2)球的半径R.
| 6 |
(1)棱锥的全面积;
(2)球的半径R.
(1)设正三棱锥的底面中心为H,
由题意知PH=1,取BC中点E,
连接HE、PE,
则HE=
,侧面的高PE=
,
S全=3×
×2
×
+
×2
×2
×
=9
+6
.
(2)过O作OG⊥PE于点G,
则△POG∽△PEH,且OG=OH=R,
∴
=
,
∴R=
-2.

由题意知PH=1,取BC中点E,
连接HE、PE,
则HE=
| 2 |
| 3 |
S全=3×
| 1 |
| 2 |
| 6 |
| 3 |
| 1 |
| 2 |
| 6 |
| 6 |
| ||
| 2 |
=9
| 2 |
| 3 |
(2)过O作OG⊥PE于点G,
则△POG∽△PEH,且OG=OH=R,
∴
| 1-R | ||
|
| R | ||
|
∴R=
| 6 |


练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 是球心
是球心 的半径
的半径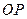 的中点,分别过
的中点,分别过 作垂直于
作垂直于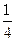


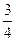


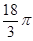


 为平面,
为平面, 为直线,则
为直线,则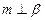 的一个充分条件是
的一个充分条件是



