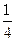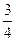题目内容
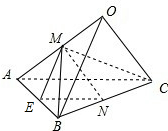
已知三棱锥O-ABC,OA=5,OB=4,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M、N分别是棱OA、BC的中点,则MN=______.
OA=5,OC=3,∠COA=90°,由勾股定理,AC=
,
取AB中点E,连结EN,ME,MC,
则ME和EN分别是三角形AOB和三角形ABC中位线,ME=2,EN=
,
在三角形OBM中,根据余弦定理,MB=
=
,
在三角形OMC中,根据勾股定理,MC=
=
,
在三角形OBC中,根据余弦定理,BC=
=
,
在三角形MBC中,根据“平行四边形中对角线的平方和等于四条边的平方和”,可得4MN2+13=2(
+
)
∴MN=
.
| 34 |
取AB中点E,连结EN,ME,MC,
则ME和EN分别是三角形AOB和三角形ABC中位线,ME=2,EN=
| ||
| 2 |
在三角形OBM中,根据余弦定理,MB=
16+
|
| 7 |
| 2 |
在三角形OMC中,根据勾股定理,MC=
|
| ||
| 2 |
在三角形OBC中,根据余弦定理,BC=
9+16-2•3•4•
|
| 13 |
在三角形MBC中,根据“平行四边形中对角线的平方和等于四条边的平方和”,可得4MN2+13=2(
| 49 |
| 4 |
| 61 |
| 4 |
∴MN=
| ||
| 2 |


练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 ,D是线段A1B1的中点.
,D是线段A1B1的中点. 
 ⊥平面A1B1BA;
⊥平面A1B1BA; ;
; 中,棱长
中,棱长 .
. 为棱
为棱 的中点,求证:
的中点,求证: ;
; 的大小;
的大小; 到平面
到平面 的距离.
的距离. 是球心
是球心 的半径
的半径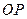 的中点,分别过
的中点,分别过 作垂直于
作垂直于