题目内容
某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
(1)求当天商店不进货的概率;
(2)记X为第二天开始营业时该商品视为件数,求X的分布列和数学期望.
(1)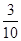 (2)X的分布列为
(2)X的分布列为X 2 3 P 

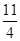
解析解:(1)P(“当天商店不进货”)=P(“当天商品销售量为0件”)+P(“当天销售量为1件”)=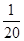 +
+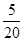 =
=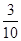 .
.
(2)由题意知,X的可能取值为2,3.
P(X=2)=P(“当天销售量为1件”)=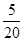 =
=
P(X=3)=P(“当天商品销售量为0件”)+P(“当天销售量为2件”)+P(“当天销售量为3件”)=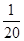 +
+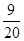 +
+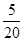 =
= .
.
故X的分布列为
所以X的数学期望为E(X)=2×X 2 3 P 

 +3×
+3× =
=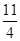 .
.

练习册系列答案
相关题目
在某次体检中,有6位同学的平均体重为65公斤.用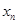 表示编号为
表示编号为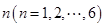 的同学的体重,且前5位同学的体重如下:
的同学的体重,且前5位同学的体重如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 体重xn | 60 | 66 | 62 | 60 | 62 |
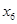 及这6位同学体重的标准差
及这6位同学体重的标准差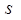 ;
;(2)从前5位同学中随机地选2位同学,求恰有1位同学的体重在区间
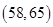 中的概率.
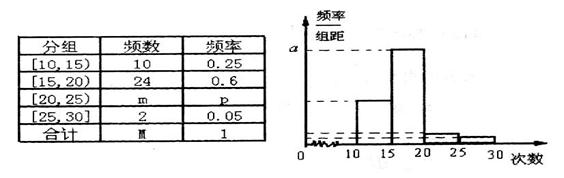
中的概率. 2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

 .
. 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学. 社区的概率;
社区的概率; 为四名同学中到
为四名同学中到 的值.
的值.