题目内容
已知函数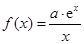 (
(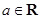 ,
,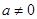 ).
).
(Ⅰ)当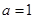 时,求曲线
时,求曲线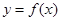 在点
在点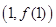 处切线的方程;
处切线的方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)当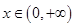 时,
时,
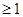 恒成立,求
恒成立,求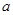 的取值范围.
的取值范围.
(Ⅰ)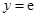 ,(Ⅱ)
,(Ⅱ) 时,函数
时,函数 的单调增区间为
的单调增区间为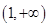 ;单调减区间为
;单调减区间为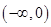 ,
,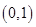 .
.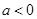 时, 函数
时, 函数 的单调增区间为
的单调增区间为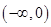 ,
,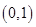 ;单调减区间为
;单调减区间为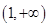 .(Ⅲ)
.(Ⅲ)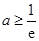
解析试题分析:(Ⅰ))利用导数的几何意义,在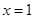 处切线的斜率为
处切线的斜率为 即为
即为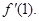 因为
因为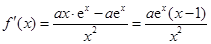 ,所以当
,所以当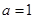 时,
时,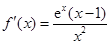 .
.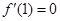 ,又
,又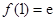 ,则曲线
,则曲线 在
在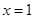 处切线的方程为
处切线的方程为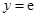 . (Ⅱ)利用导数求函数单调区间,需明确定义域
. (Ⅱ)利用导数求函数单调区间,需明确定义域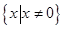 ,再导数值的符号确定单调区间. (1)若
,再导数值的符号确定单调区间. (1)若 ,当
,当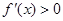 ,即
,即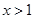 时,函数
时,函数 为增函数;当
为增函数;当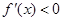 ,即
,即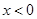 和
和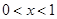 时,函数
时,函数 为减函数. 若
为减函数. 若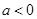 ,当
,当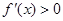 ,即
,即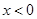 和
和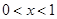 时,函数
时,函数 为增函数;当
为增函数;当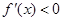 ,即
,即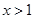 时,函数
时,函数 为减函数.(Ⅲ)不等式恒成立问题,一般利用变量分离转化为最值问题. 当
为减函数.(Ⅲ)不等式恒成立问题,一般利用变量分离转化为最值问题. 当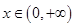 时,要使
时,要使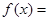
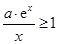 恒成立,即使
恒成立,即使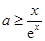 在
在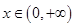 时恒成立. 设
时恒成立. 设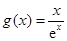 ,易得
,易得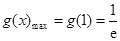 ,从而
,从而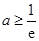 .
.
(Ⅰ)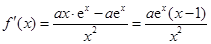 ,
,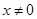 .
.
当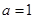 时,
时,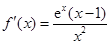 .
.
依题意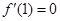 ,即在
,即在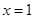 处切线的斜率为
处切线的斜率为 .
.
把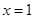 代入
代入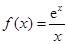 中,得
中,得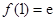 .
.
则曲线 在
在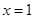 处切线的方程为
处切线的方程为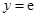 . .4分
. .4分
(Ⅱ)函数 的定义域为
的定义域为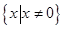 .
.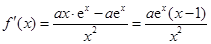 .
.
(1)若 ,
,
当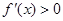 ,即
,即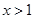 时,函数
时,函数 为增函数;
为增函数;
当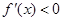 ,即
,即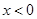 和
和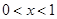 时,函数
时,函数 为减函数.
为减函数.
(2)若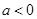 ,
,
当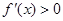 ,即
,即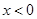 和
和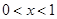 时,函数
时,函数 为增函数;
为增函数;
当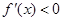 ,即
,即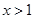 时,函数
时,函数 为减函数.
为减函数.
综上所述, 时,函数
时,函数 的单调增区间为
的单调增区间为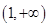

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
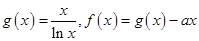 .
.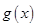 的单调区间;
的单调区间;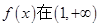 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;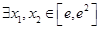 ,使
,使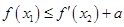 成立,求实数a的取值范围.
成立,求实数a的取值范围.
 .
. 在点
在点 处的切线方程是y=x+ln2时,求a的值.
处的切线方程是y=x+ln2时,求a的值. 在
在 处的切线的斜率为
处的切线的斜率为 .
. 的值及函数
的值及函数 的最大值;
的最大值; .
. 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.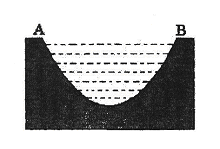
 .
. 且
且 ,
, 时,试用含
时,试用含 的式子表示
的式子表示 ,并讨论
,并讨论 的单调区间;
的单调区间; 有零点,
有零点, ,且对函数定义域内一切满足
,且对函数定义域内一切满足 的实数
的实数 有
有 .
. 时,求函数
时,求函数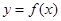 的图像与函数
的图像与函数 的图像的交点坐标.
的图像的交点坐标. .
. 时,求函数
时,求函数 的单调增区间;
的单调增区间; 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值; 图象为曲线
图象为曲线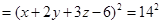 ,设点
,设点 ,
,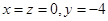 是曲线
是曲线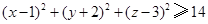 上不同的两点,点
上不同的两点,点 为线段
为线段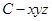 的中点,过点
的中点,过点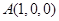 作
作 轴的垂线交曲线
轴的垂线交曲线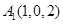 于点
于点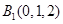 .试问:曲线
.试问:曲线 在点
在点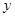 处的切线是否平行于直线
处的切线是否平行于直线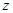 ?并说明理由.
?并说明理由. ,其中b≠0.
,其中b≠0. 时,判断函数
时,判断函数 在定义域上的单调性:
在定义域上的单调性: