题目内容
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.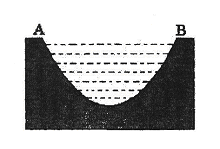
(1)6,(2)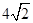 .
.
解析试题分析:(1)由题意得:保持其缺口宽度不变,需在A,B点处分别作抛物线的切线. 以抛物线顶点为原点,对称轴为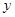 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则 ,从而边界曲线的方程为
,从而边界曲线的方程为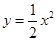 ,
,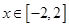 .因为抛物线在点
.因为抛物线在点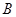 处的切线斜率
处的切线斜率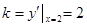 ,所以,切线方程为
,所以,切线方程为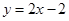 ,与
,与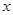 轴的交点为
轴的交点为 .此时梯形的面积
.此时梯形的面积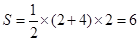 平方分米,即为所求.(2)若保持其缺口深度不变,需使两腰分别为抛物线的切线. 设梯形腰所在直线与抛物线切于
平方分米,即为所求.(2)若保持其缺口深度不变,需使两腰分别为抛物线的切线. 设梯形腰所在直线与抛物线切于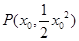 时面积最小.此时,切线方程为
时面积最小.此时,切线方程为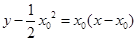 ,其与直线
,其与直线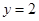 相交于
相交于 ,与
,与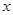 轴相交于
轴相交于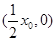 .此时,梯形的面积
.此时,梯形的面积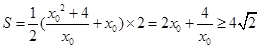 ,
,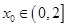 .故,当
.故,当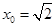 时,面积有最小值为
时,面积有最小值为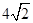 .
.
解:(1)以抛物线顶点为原点,对称轴为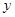 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则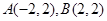 ,
,
从而边界曲线的方程为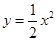 ,
,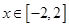 .
.
因为抛物线在点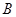 处的切线斜率
处的切线斜率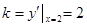 ,
,
所以,切线方程为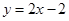 ,与
,与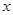 轴的交点为
轴的交点为 .
.
此时梯形的面积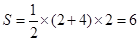 平方分米,即为所求.
平方分米,即为所求.
(2)设梯形腰所在直线与抛物线切于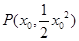 时面积最小.
时面积最小.
此时,切线方程为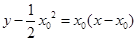 ,
,
其与直线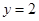 相交于
相交于 ,
,
与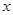 轴相交于
轴相交于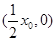 .
.
此时,梯形的面积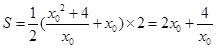 ,
,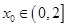 .……11分
.……11分
(这儿也可以用基本不等式,但是必须交代等号成立的条件)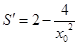 =0,得
=0,得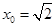 ,
,
当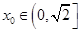 时,
时,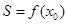 单调递减;
单调递减;
当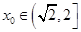 时,
时,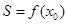 单调递增,
单调递增,
故,当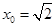 时,面积有最小值为
时,面积有最小值为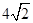 .
.
考点:利用导数研究函数最值

练习册系列答案
相关题目
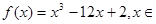 R,求函数
R,求函数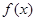 在区间
在区间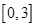 上的最小值.
上的最小值.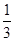 ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.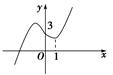
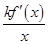 -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.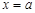 和
和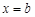 是函数
是函数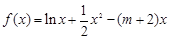 的两个极值点,其中
的两个极值点,其中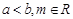 .
.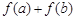 的取值范围;
的取值范围;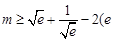 为自然对数的底数),求
为自然对数的底数),求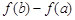 的最大值.
的最大值.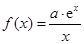 (
( ,
, ).
).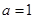 时,求曲线
时,求曲线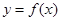 在点
在点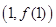 处切线的方程;
处切线的方程; 的单调区间;
的单调区间;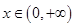 时,
时,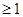 恒成立,求
恒成立,求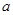 的取值范围.
的取值范围.
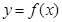 的单调区间;
的单调区间;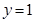 恰有两个交点,求
恰有两个交点,求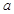 的取值范围.
的取值范围.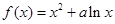 图象与直线
图象与直线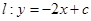 相切,切点横坐标为
相切,切点横坐标为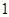 .
.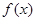 的表达式和直线
的表达式和直线 的方程;(2)求函数
的方程;(2)求函数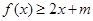 对
对 恒成立,求实数
恒成立,求实数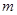 的取值范围.
的取值范围.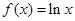 ,
,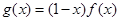
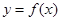 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;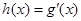 及
及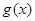 在区间
在区间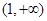 上的单调性;
上的单调性;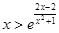 在
在 函数
函数 在
在 上是单调递减函数,
上是单调递减函数, 方程
方程 无实根,若“
无实根,若“ 或
或 ”为真,“
”为真,“ 的取值范围。
的取值范围。