题目内容
设a，b，c是三角形ABC的边长，对任意实数x，f（x）=b2x2+（b2+c2-a2）x+c2有（ ）
| A．f（x）=0 | B．f（x）＞0 | C．f（x）≥0 | D．f（x）＜0 |
在△ABC中，根据余弦定理a2=b2+c2-2bccosA，
∴b2+c2-a2=2bccosA，
因此函数可化为：f（x）=b2x2+（2bccosA）x+c2，
∵
，
∴函数y=f（x）的图象是开口向上的抛物线，且与x轴没有公共点．
由此可得：对任意实数x，f（x）＞0恒成立．
故选：B
∴b2+c2-a2=2bccosA，
因此函数可化为：f（x）=b2x2+（2bccosA）x+c2，
∵
|
∴函数y=f（x）的图象是开口向上的抛物线，且与x轴没有公共点．
由此可得：对任意实数x，f（x）＞0恒成立．
故选：B
练习册系列答案
阅读快车系列答案
相关题目
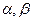是同一三角形的两个内角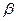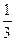，cos
=" -" 
,cos(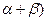
=-
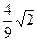.求cot
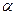的值．
