题目内容
△ABC中
(1)已知2B=A+C,b=1,求a+c的范围
(2)已知2asinA=(2b+c)sinB+(2c+b)sinC,且sinB+sinC=1,判断△ABC的形状.
(1)已知2B=A+C,b=1,求a+c的范围
(2)已知2asinA=(2b+c)sinB+(2c+b)sinC,且sinB+sinC=1,判断△ABC的形状.
(1)∵△ABC中,2B=A+C,
∴A+B+C=π,即B=
,
∵b=1,∴由正弦定理得:2R=
=
=
,
∵A+C=
,即C=
-A,
∴a+c=2RsinA+2RsinC=2R(sinA+sinC)=
[sinA+sin(
-A)]=
2sin
cos(A-
)=4cos(A-
),
∵0<A<
,∴-
<A-
<
,
∴
<cos(A-
)<1,即2<4cos(A-
)<4,
则a+c的范围是(2,4);
(2)已知等式利用正弦定理化简得:2a2=b(2b+c)+c(2c+b),即b2+c2-a2=-bc,
∴cosA=
=
=-
,
∵A为三角形内角,∴A=120°,即B+C=60°,
∴sinB+sinC=sinB+sin(60°-B)=2sin30°cos(B-30°)=cos(B-30°)=1,
∴B-30°=0,即B=30°,
则△ABC为等腰三角形.
∴A+B+C=π,即B=
| π |
| 3 |
∵b=1,∴由正弦定理得:2R=
| b |
| sinB |
| 1 | ||||
|
2
| ||
| 3 |
∵A+C=
| 2π |
| 3 |
| 2π |
| 3 |
∴a+c=2RsinA+2RsinC=2R(sinA+sinC)=
4
| ||
| 3 |
| 2π |
| 3 |
4
| ||
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵0<A<
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
则a+c的范围是(2,4);
(2)已知等式利用正弦定理化简得:2a2=b(2b+c)+c(2c+b),即b2+c2-a2=-bc,
∴cosA=
| b2+c2-a2 |
| 2bc |
| -bc |
| 2bc |
| 1 |
| 2 |
∵A为三角形内角,∴A=120°,即B+C=60°,
∴sinB+sinC=sinB+sin(60°-B)=2sin30°cos(B-30°)=cos(B-30°)=1,
∴B-30°=0,即B=30°,
则△ABC为等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
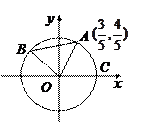
 、
、 是单位圆
是单位圆 上的动点,
上的动点, 是圆与
是圆与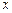 轴正半轴的交点,设
轴正半轴的交点,设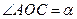 .
.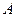 的坐标为
的坐标为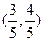 时,求
时,求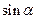 的值;
的值;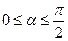 ,且当点A、B在圆上沿逆时针方向移动时总有
,且当点A、B在圆上沿逆时针方向移动时总有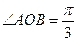 ,试求
,试求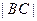 的取值范围.
的取值范围. 0
0