题目内容
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点P
,点P![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)设![]() 分别为椭圆C的左右焦点,过
分别为椭圆C的左右焦点,过![]() 的直线
的直线![]() 与椭圆C交于不同的两点A、B,求△
与椭圆C交于不同的两点A、B,求△![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
【答案】(1) ![]() ;(2) 最大值为
;(2) 最大值为![]() .
.
【解析】
(1) 根据离心率为![]() ,点
,点![]() 在椭圆上,结合性质
在椭圆上,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() ,即可得结果;(2)可设直线
,即可得结果;(2)可设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,可得
,与椭圆方程联立,可得![]() ,结合韦达定理、弦长公式,利用三角形面积公式可得
,结合韦达定理、弦长公式,利用三角形面积公式可得![]() ,换元后利用导数可得
,换元后利用导数可得![]() 的最大值为
的最大值为![]() ,再结
,再结![]() 可得结果.
可得结果.
(1)依题意有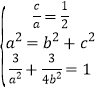 ,解得
,解得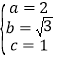 ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,设
,设![]() 的内切圆半径为
的内切圆半径为![]() ,
,
![]() 的周长为
的周长为![]() ,
,
![]() ,
,
根据题意知,直线![]() 的斜率不为零,
的斜率不为零,
可设直线![]() 的方程为
的方程为![]() ,
,
由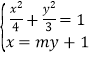 ,得
,得![]() ,
,
![]() ,
,
由韦达定理得![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
令![]() ,则当
,则当![]() 时,
时,![]() 单调递增,
单调递增,
![]() ,
,
即当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,
,
故当直线![]() 的方程为
的方程为![]() 时,
时,![]() 内切圆半径的最大值为
内切圆半径的最大值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资![]() (单位:元)与月销售产品件数
(单位:元)与月销售产品件数![]() 的函数关系式;
的函数关系式;
(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.