题目内容
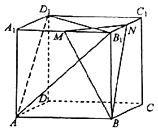
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AB⊥AD，AD∥BC，AD= 
BC=2，E在BC上，且BE= AB=1，侧棱PA⊥平面ABCD．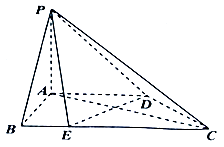 
（1）求证：平面PDE⊥平面PAC；
（2）若△PAB为等腰直角三角形． （i）求直线PE与平面PAC所成角的正弦值；
（ii）求二面角A﹣PC﹣D的余弦值．
【答案】
（1）证明：∵PA⊥平面ABCD，∴AB⊥PA，
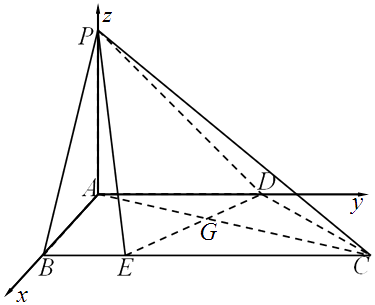
又∵AB⊥AD，故可建立建立如图所示坐标系．
由已知D（0，2，0），E（2，1，0），C（2，4，0），P（0，0，λ），（λ＞0）
∴ 
=（2，4，0）， 
=（0，0，λ）， 
=（2，﹣1，0），
∴ 
=4﹣4+0=0， 
．，
∴DE⊥AC，DE⊥AP，∴ED⊥平面PAC，
∵ED平面PDE，平面PDE⊥平面PAC
（2）解：（i）由（1）得，平面PAC的一个法向量是 =（2，﹣1，0），
∵△PAB为等腰直角三角形，故PA=2， 
．
设直线PE与平面PAC所成的角为θ，
则 
= 
= 
= 
，
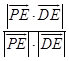∴直线PE与平面PAC所成角的正弦值为 ．
（ii）设平面PCD的一个法向量为 
=（x，y，z），
=（2，2，0）， 
=（0，﹣2，2），
则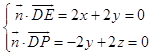 
，令x=1，则 =（1，﹣1，﹣1），
∴cos＜ 
＞= 
= 
．
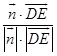∵二面角A﹣PC﹣D的平面角是锐角，
∴二面角A﹣PC﹣D的余弦值为 
．
【解析】（1）由AB⊥PA，AB⊥AD，建立建立空间直角坐标系，利用向量法能证明平面PDE⊥平面PAC．（2）（i）求出平面PAC的一个法向量和 ，利用向量法能求出直线PE与平面PAC所成角的正弦值．（ii）求出平面PCD的一个法向量，利用向量法能求出二面角A﹣PC﹣D的余弦值．
【考点精析】认真审题，首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线，则这两个平面垂直)，还要掌握空间角的异面直线所成的角(已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则
)的相关知识才是答题的关键．
