题目内容
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上.
=1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上. 
(1)求椭圆C的方程;
(2)设点M(2,0),过点F1的直线交C于A,B两点,直线MA,MB与直线x=﹣2分别交于P,Q两点,求△MPQ面积的最大值.
【答案】
(1)解:由题意可得  ,解得a2=2,b2=1,
,解得a2=2,b2=1,
∴椭圆方程为 ![]() ;
;
(2)解:设过点F1 的直线AB为x=my﹣1,代入椭圆方程 ![]() ,
,
得(m2+2)y2﹣2my﹣1=0,
设A(x1,y1),B(x2,y2),
则 ![]() ,
,
由M,A,P三点共线,得 ![]() ,同理
,同理 ![]() ,
,
则△MPQ的面积 ![]()
= 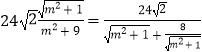 ≤6.
≤6.
故当m2=7时,△MPQ面积的最大值为6
【解析】(1)由题意列关于a,b,c的方程组,求解方程组得到a,b,c的值,则椭圆方程可求;(2)设出过点F1 的直线AB为x=my﹣1,联立直线方程和椭圆方程,化为关于y的一元二次方程,利用根与系数的关系求出P,Q的纵坐标,代入三角形面积公式,利用基本不等式求最值.

练习册系列答案
相关题目