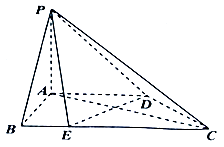
题目内容
【题目】如图,在六面体ABCD﹣A1B1C1D1中,M,N分别是棱A1B1 , B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1 . 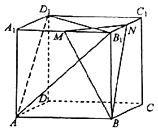
(1)证明:BB1⊥平面ABCD;
(2)已知六面体ABCD﹣A1B1C1D1的棱长均为 ![]() ,cos∠BAD=
,cos∠BAD= ![]() ,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
【答案】
(1)证明:过点D作DP⊥AB,过点D作DQ⊥BC,
由平面ABCD⊥平面A1B1BA,BB1平面A1B1BA,
得DP⊥BB1,
由平面ABCD⊥平面B1BCC1,BB1平面B1BCC1,
得DQ⊥BB1,
又DP∩DQ=D,∴BB1⊥平面ABCD
(2)解:由AB=AD= ![]() ,且cos∠BAD=
,且cos∠BAD= ![]() ,
,
在△ABD中利用余弦定理得BD=2,
设AC与BD的交点为O, ![]() 与B1D1的交点为O1,
与B1D1的交点为O1,
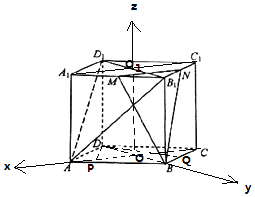
以O为原点,分别以OA,OB,OO1所在直线为x,y,z轴,
建立空间直角坐标系,
则B(0,1,0),M(1, ![]() ,
, ![]() ),N(﹣1,
),N(﹣1, ![]() ,
, ![]() ),
),
C(﹣2,0,0),A1(2,0, ![]() ),A(2,0,0),
),A(2,0,0),
B1(0,1, ![]() ),D1(0,﹣1,
),D1(0,﹣1, ![]() ),
),
设平面BMN的法向量为 ![]() =(a,b,c),
=(a,b,c),
![]() =(1,﹣
=(1,﹣ ![]() ,
, ![]() ),
), ![]() =(﹣2,0,0),
=(﹣2,0,0),
则 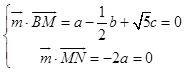 ,取b=10,得
,取b=10,得 ![]() =(0,10,
=(0,10, ![]() ),
),
设平面AB1D1的法向量为 ![]() =(x,y,z),
=(x,y,z),
![]() =(﹣2,1,
=(﹣2,1, ![]() ),
), ![]() =(0,﹣2,0),
=(0,﹣2,0),
则 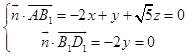 ,取x=5,得
,取x=5,得 ![]() =(5,0,2
=(5,0,2 ![]() ),
),
∴cosθ= ![]() =
= ![]() .
.
【解析】(1)过点D作DP⊥AB,过点D作DQ⊥BC,推导出DP⊥BB1 , DQ⊥BB1 , 由此能证明BB1⊥平面ABCD.(2)设AC与BD的交点为O, ![]() 与B1D1的交点为O1 , 以O为原点,分别以OA,OB,OO1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出cosθ.
与B1D1的交点为O1 , 以O为原点,分别以OA,OB,OO1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出cosθ.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】某公司准备将1000万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润ξ1(万元)的概率分布列如表所示:
ξ1 | 110 | 120 | 170 |
P | m | 0.4 | n |
且ξ1的期望E(ξ1)=120;若投资乙项目一年后可获得的利润ξ2(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为p(0<p<1)和1﹣p.若乙项目产品价格一年内调整次数X(次数)与ξ2的关系如表所示:
X | 0 | 1 | 2 |
ξ2 | 41.2 | 117.6 | 204.0 |
(Ⅰ)求m,n的值;
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.