题目内容
【题目】给出以下四个结论:
①函数![]() 是偶函数;
是偶函数;
②当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ;
;
③若扇形的周长为![]() ,圆心角为
,圆心角为![]() ,则该扇形的弧长为6cm;
,则该扇形的弧长为6cm;
④已知定义域为![]() 的函数
的函数![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
⑤函数![]() 的最小正周期是
的最小正周期是![]()
则上述结论中正确的是______(写出所有正确结论的序号)
【答案】②④
【解析】
利用特殊值代入①中的解析式即可判断①;根据函数单调性及自变量取值范围,可判断②;根据扇形的周长及圆心角即可求得半径,进而求得弧长,可判断③;讨论sinx﹣cosx的符号去绝对值,即可判断④;利用周期性定义验证![]() ,即可判断⑤.
,即可判断⑤.
解:当x![]() 与x
与x![]() 时,代入①中的解析式所得函数值不相等,所以①错误;
时,代入①中的解析式所得函数值不相等,所以①错误;
当x∈[0,![]() ]时,2x
]时,2x![]() x∈[
x∈[![]() ,
,![]() ],
],
由余弦函数图象可知函数f(x)=2cos(2x![]() )的值域是[﹣2,
)的值域是[﹣2,![]() ];所以②正确;
];所以②正确;
因为若扇形的周长为15cm,圆心角为![]() rad,设半径为r,
rad,设半径为r,
则15﹣2r![]() r,解得r=6,所以弧长为l=ar=3 cm,所以③错误;
r,解得r=6,所以弧长为l=ar=3 cm,所以③错误;
当sinx﹣cosx≥0时,函数f(x)![]() cosx,
cosx,
2kπ<x<2kπ![]() (k∈Z)时,f(x)>0;
(k∈Z)时,f(x)>0;
当sinx﹣cosx<0时,函数f(x)![]() sinx,
sinx,
2kπ<x<2kπ![]() (k∈Z)时,f(x)>0,所以④正确.
(k∈Z)时,f(x)>0,所以④正确.
记![]() ,
,![]() ,
,
![]() ,
,
![]() ,故
,故![]() 也是函数的周期,故⑤错误,
也是函数的周期,故⑤错误,
综上所述,②④正确.
故答案为:②④.

练习册系列答案
相关题目
【题目】抽样得到某次考试中高二年级某班![]() 名学生的数学成绩和物理成绩如下表:
名学生的数学成绩和物理成绩如下表:
学生编号 |
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
物里成绩 |
|
|
|
|
|
|
(1)在图中画出表中数据的散点图;
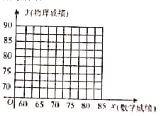
(2)建立![]() 关于
关于![]() 的回归方程:(系数保留到小数点后两位).
的回归方程:(系数保留到小数点后两位).
(3)如果某学生的数学成绩为![]() 分,预测他本次的物理成绩(成绩取整数).
分,预测他本次的物理成绩(成绩取整数).
参考公式:回归方程为![]() ,其中
,其中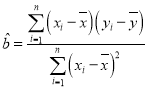 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.