题目内容
函数f(x)是幂函数,图象过点(2,8),定义在实数R上的函数y=F(x)是奇函数,当x>0时,F(x)=f(x)+1,求F(x)在R上的表达式;并画出图象.
设y=xα,(x>0);
将(2,8)代入得α=3,
当x>0,F(x)=f(x)+1=x3+1,
当x<0,-x>0,F(-x)=(-x)3+1=-x3+1,
∵y=F(x)是奇函数,∴F(-X)=-F(X)∴F(x)=x3-1,
∵y=F(x)是定义在实数R上的奇函数,
∴F(0)=0.
∴F(x)=
.
图象见右图:

将(2,8)代入得α=3,
当x>0,F(x)=f(x)+1=x3+1,
当x<0,-x>0,F(-x)=(-x)3+1=-x3+1,
∵y=F(x)是奇函数,∴F(-X)=-F(X)∴F(x)=x3-1,
∵y=F(x)是定义在实数R上的奇函数,
∴F(0)=0.
∴F(x)=
|
图象见右图:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 是奇函数,且当
是奇函数,且当 时,
时, ,则
,则 = 。
= 。 与方程
与方程 (其中e是自然对数的底数)的所有根之和为
(其中e是自然对数的底数)的所有根之和为 ,则( )
,则( )



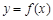 ,
,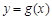 均存在反函数,并且函数
均存在反函数,并且函数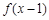 与
与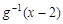 的图像关于直线
的图像关于直线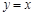 对称,若
对称,若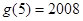 ,则
,则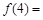
 的反函数是
的反函数是 则
则 。
。