题目内容
若直线 与圆
与圆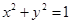 相离,则点
相离,则点 的位置是
的位置是
 与圆
与圆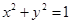 相离,则点
相离,则点 的位置是
的位置是| A.在圆上 | B.在圆外 | C.在圆内 | D.以上都有可能 |
C
专题:计算题.
分析:根据直线与圆的位置关系,得到圆心到直线的距离大于半径,得到关于a,b的关系式,这个关系式正好是点到圆心的距离,得到圆心与点到距离小于半径,得到点在圆的内部.
解答:解:∵直线ax+by+1=0与圆x2+y2=1相离,
∴
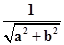 >1,
>1,∴
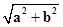 <1,
<1,∴点P(a,b)到圆心的距离小于半径,
∴点在圆内,
故选C.
点评:本题考查直线与圆的位置关系和点与圆的位置关系,本题解题的关键是正确利用点到直线的距离公式,本题是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
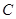 的方程为
的方程为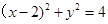 ,圆
,圆 的方程为
的方程为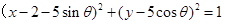
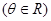 ,过圆
,过圆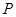 作圆
作圆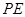 、
、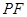 ,切点分别为
,切点分别为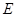 、
、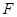 ,则
,则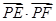 的最小值是( )
的最小值是( )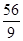
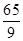
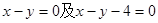 都相切,圆心在直线
都相切,圆心在直线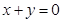 上,则圆C的方程为()
上,则圆C的方程为() 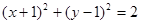
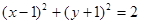
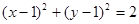
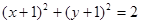
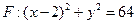 (F为圆心
(F为圆心 )上一点,线段AB的垂直平分线交BF于P.
)上一点,线段AB的垂直平分线交BF于P. 

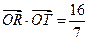 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.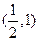 的直线l与圆C
的直线l与圆C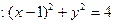 交于A、B两点,当∠ACB最小时,直线l的方程为 ( )
交于A、B两点,当∠ACB最小时,直线l的方程为 ( )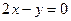 B.
B.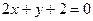 C.
C.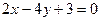 D.
D.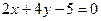
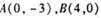 ,若点P是圆
,若点P是圆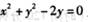 上的动点,则
上的动点,则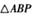 面积的最小值为
面积的最小值为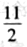
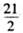
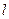 经过坐标原点,且与圆
经过坐标原点,且与圆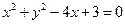 相切,切点在第四象限,则直线
相切,切点在第四象限,则直线