题目内容
.圆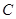 的方程为
的方程为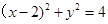 ,圆
,圆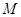 的方程为
的方程为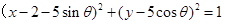
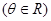 ,过圆
,过圆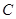 上任意一点
上任意一点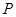 作圆
作圆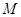 的两条切线
的两条切线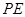 、
、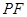 ,切点分别为
,切点分别为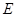 、
、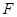 ,则
,则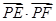 的最小值是( )
的最小值是( )
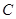 的方程为
的方程为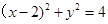 ,圆
,圆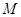 的方程为
的方程为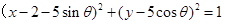
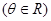 ,过圆
,过圆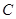 上任意一点
上任意一点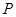 作圆
作圆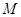 的两条切线
的两条切线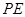 、
、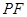 ,切点分别为
,切点分别为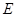 、
、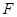 ,则
,则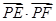 的最小值是( )
的最小值是( )| A.6 | B.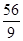 | C.7 | D.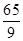 |
B
分析:由两圆的圆心距|CM|=5大于两圆的半径之和可得两圆相离,如图所示,则
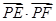 的最小值是
的最小值是 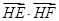 ,利用两个向量的数量积的定义求出
,利用两个向量的数量积的定义求出 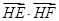 的值,即为所求.
的值,即为所求.解:(x-2)2+y2=4的圆心C(2,0),半径等于2,圆M (x-2-5sinθ)2+(y-5cosθ)2=1,
圆心M(2+5sinθ,5cosθ),半径等于1.∵|CM|=
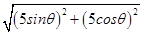 =5>2+1,故两圆相离.
=5>2+1,故两圆相离.∵
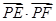 =
=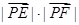 ?cos∠EPF,要使
?cos∠EPF,要使 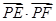 最小,需
最小,需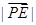 和
和 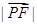 最小,且∠EPF 最大,
最小,且∠EPF 最大,如图所示,设直线CM 和圆C 交于H、G两点,则
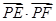 的最小值是
的最小值是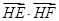 .
.|H M|=|CM|-2=5-2=3,|H E|=
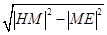 =
=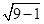 =2
=2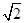 ,sin∠MHE=
,sin∠MHE=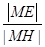 =
=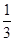 ,
,∴cos∠EHF=cos2∠MHE=1-2sin2∠MHE=
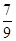 ,
,∴
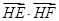 ="|H" E|?|H E|?cos∠EHF=2
="|H" E|?|H E|?cos∠EHF=2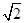 ×2
×2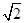 ×
×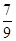 =
=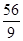 ,故选 B.
,故选 B.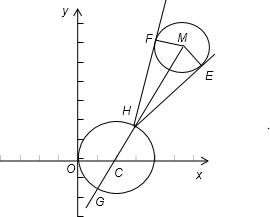

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
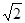 ,AD=
,AD=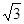 ,则∠CAD的弧度数为 .
,则∠CAD的弧度数为 . 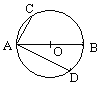
 与圆
与圆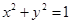 相离,则点
相离,则点 的位置是
的位置是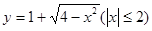 与直线
与直线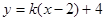 有两个交点时,实数k的取值范围是 ( )
有两个交点时,实数k的取值范围是 ( )
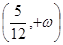
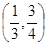

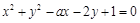 关于直线x – y – 1 = 0对称的圆的方程是
关于直线x – y – 1 = 0对称的圆的方程是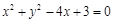 ,则a的值等于( )
,则a的值等于( )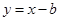 与曲线
与曲线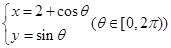 有两个不同的公共点,则实数
有两个不同的公共点,则实数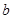 的取值范围为
的取值范围为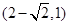
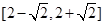
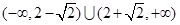
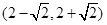
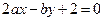 (
(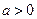 ,
,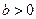 )被圆
)被圆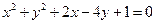 截得的
截得的 弦长为4,则
弦长为4,则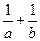 的最小值为( )
的最小值为( )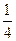


 .
.