题目内容
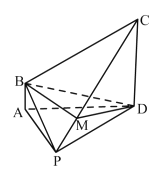
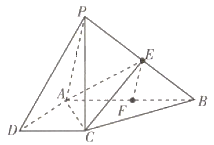
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,F是
,F是![]() 的中点,E是
的中点,E是![]() 上的一点,则下列说法正确的是( )
上的一点,则下列说法正确的是( )
A.若![]() ,则
,则![]() 平面
平面![]()
B.若![]() ,则四棱锥
,则四棱锥![]() 的体积是三棱锥
的体积是三棱锥![]() 体积的6倍
体积的6倍
C.三棱锥![]() 中有且只有三个面是直角三角形
中有且只有三个面是直角三角形
D.平面![]() 平面
平面![]()
【答案】AD
【解析】
利用中位线的性质即可判断选项A;先求得四棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 的体积的关系,再由四棱锥
的体积的关系,再由四棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的关系进而判断选项B;由线面垂直的性质及勾股定理判断选项C;先证明
的关系进而判断选项B;由线面垂直的性质及勾股定理判断选项C;先证明![]() 平面
平面![]() ,进而证明平面
,进而证明平面![]() 平面
平面![]() ,即可判断选项D.
,即可判断选项D.
对于选项A,因为![]() ,所以
,所以![]() 是
是![]() 的中点,
的中点,
因为F是![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故A正确;
,故A正确;
对于选项B,因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,
所以梯形![]() 的面积为
的面积为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,故B错误;
,故B错误;
对于选项C,因为![]() 底面
底面![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() 为直角三角形,
为直角三角形,
又![]() ,所以
,所以![]() ,则
,则![]() 为直角三角形,
为直角三角形,
所以![]() ,
,![]() ,
,
则![]() ,所以
,所以![]() 是直角三角形,
是直角三角形,
故三棱锥![]() 的四个面都是直角三角形,故C错误;
的四个面都是直角三角形,故C错误;
对于选项D,因为![]() 底面
底面![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,
在直角梯形![]() 中,
中,![]() ,
,
所以![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,故D正确,
,故D正确,
故选:AD

练习册系列答案
相关题目