题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 的最大值与最小值;
的最大值与最小值;
(2)若![]() 对任意的
对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)直接求出函数的导数,通过导数为0,求出函数的极值点,判断函数的单调性,利用最值定理求出f(x)的最大值与最小值;
(2)利用(1)的结论,f(x)<4-At于任意的x∈[1,3],t∈[0,2]恒成立,转化为4-At>![]() 对任意t∈[0,2]恒成立,通过
对任意t∈[0,2]恒成立,通过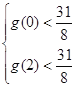 求实数A的取值范围.
求实数A的取值范围.
试题解析:(1)因为函数f(x)=![]() ﹣lnx,
﹣lnx,
所以f′(x)=![]() ,令f′(x)=0得x=±2,
,令f′(x)=0得x=±2,
因为x∈[1,3],
当1<x<2时 f′(x)<0;当2<x<3时,f′(x)>0;
∴f(x)在(1,2)上单调减函数,在(2,3)上单调增函数,
∴f(x)在x=2处取得极小值f(2)=![]() ﹣ln2;
﹣ln2;
又f(1)=![]() ,f(3)=
,f(3)=![]() ,
,
∵ln3>1∴![]()
∴f(1)>f(3),
∴x=1时 f(x)的最大值为![]() ,
,
x=2时函数取得最小值为![]() ﹣ln2.
﹣ln2.
(2)由(1)知当x∈[1,3]时,f(x)![]() ,
,
故对任意x∈[1,3],f(x)<4﹣At恒成立,
只要4﹣At>![]() 对任意t∈[0,2]恒成立,即At
对任意t∈[0,2]恒成立,即At![]() 恒成立
恒成立
记 g(t)=At,t∈[0,2]
∴,解得A![]() ,
,
∴实数A的取值范围是(﹣∞,![]() ).
).

【题目】某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )
表1
成绩 | 不及格 | 及格 | 总计 |
男 | 6 | 14 | 20 |
女 | 10 | 22 | 32 |
总计 | 16 | 36 | 52 |
表2
视力 | 好 | 差 | 总计 |
男 | 4 | 16 | 20 |
女 | 12 | 20 | 32 |
总计 | 16 | 36 | 52 |
表3
智商 | 偏高 | 正常 | 总计 |
男 | 8 | 12 | 20 |
女 | 8 | 24 | 32 |
总计 | 16 | 36 | 52 |
表4
阅读量 | 丰富 | 不丰富 | 总计 |
男 | 14 | 6 | 20 |
女 | 2 | 30 | 32 |
总计 | 16 | 36 | 52 |
A.成绩
B.视力
C.智商
D.阅读量
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.
(1)大气污染可引起心悸、呼吸困难等心肺疾病. 为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
问有多大的把握认为是否患心肺疾病与性别有关?
(2)空气质量指数PM2.5(单位:μg/![]() )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重. 某市在2016年年初着手治理环境污染,改善空气质量,检测到2016年1~5月的日平均PM2.5指数如下表:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重. 某市在2016年年初着手治理环境污染,改善空气质量,检测到2016年1~5月的日平均PM2.5指数如下表:
月份x | 1 | 2 | 3 | 4 | 5 |
PM2.5指数y | 79 | 76 | 75 | 73 | 72 |
试根据上表数据,求月份x与PM2.5指数y的线性回归直线方程![]() ,并预测2016年8月份的日平均PM2.5指数 (保留小数点后一位).
,并预测2016年8月份的日平均PM2.5指数 (保留小数点后一位).
【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额![]() 关于销售额
关于销售额![]() 的回归直线方程;
的回归直线方程;
(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式: ,
,![]() ]
]
