题目内容
已知函数
(1)指出 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(2)用五点法画出它在一个周期内的闭区间上的图象;
(3)说明此函数图象可由 的图象经怎样的变换得到.
的图象经怎样的变换得到.

(1)指出
 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;(2)用五点法画出它在一个周期内的闭区间上的图象;
(3)说明此函数图象可由
 的图象经怎样的变换得到.
的图象经怎样的变换得到.
(1)周期T=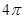 ,振幅A=3,初相
,振幅A=3,初相 ,由
,由 ,得
,得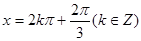 即为对称轴;
即为对称轴;
(2)列表
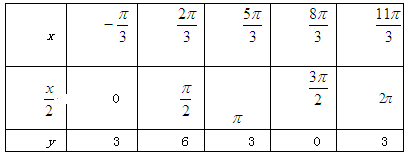

(3)①由 的图象上各点向左平移
的图象上各点向左平移 个长度单位,得
个长度单位,得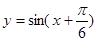 的图象;
的图象;
②由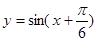 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得
的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得 的图象;
的图象;
③由 的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得
的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得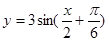 的图象;
的图象;
④由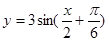 的图象上各点向上平移3个长度单位,
的图象上各点向上平移3个长度单位,
得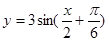 +3的图象。
+3的图象。
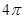 ,振幅A=3,初相
,振幅A=3,初相 ,由
,由 ,得
,得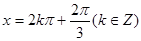 即为对称轴;
即为对称轴;(2)列表


(3)①由
 的图象上各点向左平移
的图象上各点向左平移 个长度单位,得
个长度单位,得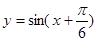 的图象;
的图象;②由
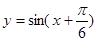 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得
的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得 的图象;
的图象;③由
 的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得
的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得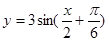 的图象;
的图象;④由
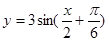 的图象上各点向上平移3个长度单位,
的图象上各点向上平移3个长度单位,得
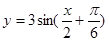 +3的图象。
+3的图象。 本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象,函数y=Asin(ωx+φ)的图象变换,其中正弦型函数的图象的画法,性质是三角函数的重点内容之一,一定要熟练掌握.
(1)分别令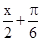 取0,π
取0,π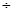 2 ,π,3π
2 ,π,3π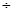 2 ,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象
2 ,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象
(2)根据函数的解析式中A=3,ω="1"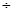 2 ,φ=π
2 ,φ=π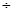 6 ,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相、对称轴;
6 ,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相、对称轴;
(3)根据正弦型函数的平移变换,周期变换及振幅变换的法则,根据函数的解析式,易得到函数图象可由y=sinx在[0,2π]上的图象经怎样的变换得到的
(1)分别令
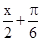 取0,π
取0,π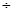 2 ,π,3π
2 ,π,3π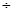 2 ,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象
2 ,2π,并求出对应的(x,d(x))点,描点后即可得到函数在一个周期内的图象(2)根据函数的解析式中A=3,ω="1"
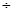 2 ,φ=π
2 ,φ=π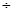 6 ,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相、对称轴;
6 ,然后根据正弦型函数的性质,即可求出f(x)的周期、振幅、初相、对称轴;(3)根据正弦型函数的平移变换,周期变换及振幅变换的法则,根据函数的解析式,易得到函数图象可由y=sinx在[0,2π]上的图象经怎样的变换得到的

练习册系列答案
相关题目
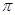 ]上满足
]上满足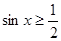 的x的取值范围是( )
的x的取值范围是( )



 的一部分图象(如右图所示),
的一部分图象(如右图所示),
 可以是( )
可以是( )







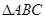 中,若
中,若 ,
, ,则角C的大小为( )
,则角C的大小为( )

 或
或
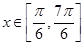 时,函数
时,函数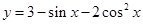 的最小值是_______,最大值是________。
的最小值是_______,最大值是________。 为单位圆在第一象限内圆弧上的动点,
为单位圆在第一象限内圆弧上的动点, ,设
,设 ,过
,过 ,并交直线
,并交直线 于点
于点 .
.
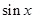 表示) ;
表示) ; 能否为
能否为 ?若能,求出点
?若能,求出点 的面积的最大值,并求出相应
的面积的最大值,并求出相应 值.
值.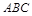 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. 的值域是 .
的值域是 .
 的最小正周期为
的最小正周期为 ,则
,则 的值为( )
的值为( )