题目内容
设数列{an}的前n项和为Sn.已知a1=a,an+1=Sn+3n,n∈N*.
(1)设bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N*,求a的取值范围.
(1)设bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N*,求a的取值范围.
(1)bn= (a-3)2n-1,n∈N*.
(2)[-9,+∞)
(2)[-9,+∞)
解:(1)依题意,Sn+1-Sn=an+1=Sn+3n,
即Sn+1=2Sn+3n,
由此得Sn+1-3n+1=2(Sn-3n),
即bn+1=2bn,b1=S1-3=a-3.
因此,所求通项公式为
bn=b1·2n-1=(a-3)2n-1,n∈N*.①
(2)由①知Sn=3n+(a-3)2n-1,n∈N*,
于是,当n≥2时,
an=Sn-Sn-1
=3n+(a-3)2n-1-3n-1-(a-3)2n-2
=2×3n-1+(a-3)2n-2,
an+1-an
=4×3n-1+(a-3)2n-2
=2n-2·[12( )n-2+a-3],
)n-2+a-3],
当n≥2时,an+1≥an?12( )n-2+a-3≥0?a≥-9.
)n-2+a-3≥0?a≥-9.
又a2=a1+3>a1.
所以a的取值范围是[-9,+∞).
即Sn+1=2Sn+3n,
由此得Sn+1-3n+1=2(Sn-3n),
即bn+1=2bn,b1=S1-3=a-3.
因此,所求通项公式为
bn=b1·2n-1=(a-3)2n-1,n∈N*.①
(2)由①知Sn=3n+(a-3)2n-1,n∈N*,
于是,当n≥2时,
an=Sn-Sn-1
=3n+(a-3)2n-1-3n-1-(a-3)2n-2
=2×3n-1+(a-3)2n-2,
an+1-an
=4×3n-1+(a-3)2n-2
=2n-2·[12(
 )n-2+a-3],
)n-2+a-3],当n≥2时,an+1≥an?12(
 )n-2+a-3≥0?a≥-9.
)n-2+a-3≥0?a≥-9.又a2=a1+3>a1.
所以a的取值范围是[-9,+∞).

练习册系列答案
相关题目
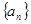 满足:
满足: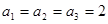 ,
,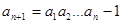 (
(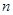 ≥3),记
≥3),记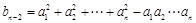
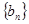 为等差数列,并求通项公式;
为等差数列,并求通项公式;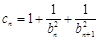 ,数列{
,数列{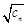 }的前n项和为
}的前n项和为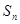 ,求证:
,求证: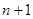 .
.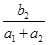 的值为________.
的值为________.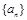 满足
满足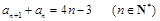 .
.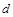 的值;
的值;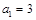 ,求数列
,求数列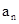 }中,若
}中,若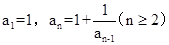 ,则
,则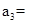 ( ).
( ).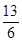
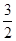
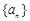 的前
的前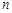 项和
项和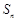 满足
满足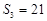 ,
,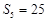 .
.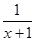 、
、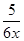 、
、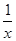 ,则数列的公差d是( )
,则数列的公差d是( )


