题目内容
【题目】某商场经营一批进价为30元/件的商品，在市场试销中发现，此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
x | … | 30 | 40 | 45 | 50 | … |
y | … | 60 | 30 | 15 | 0 | … |
(1)在所给的坐标系中，如图，根据表格提供的数据描出实数对(x，y)的对应点，并确定y与x的一个函数关系式y＝f(x)；
(2)设经营此商品的日销售利润为P元，根据上述关系，写出P关于x的函数关系式，并指出销售单价x为多少时，才能获得最大日销售利润？
【答案】（1）y＝－3x＋150，(x∈N)；（2）销售价为40元时，才能获得最大利润.
【解析】试题分析：（1）由题意画出所给的点，结合题意求解一次函数的解析式即可；
（2）结合（1）的结论和二次函数的性质整理计算即可求得最终结果．
试题解析：
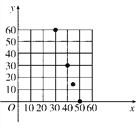
(1)由表作出点(30，60)，(40，30)，(45，15)，(50，0).如图，它们近似地在一条直线上，设它们共线于直线y＝kx＋b，
∴
解得
∴y＝－3x＋150，(x∈N).
经检验(30，60)，(40，30)也在此直线上.
∴所求函数解析式为y＝－3x＋150，(x∈N).
(2)依题意P＝y(x－30)＝(－3x＋150)(x－30)＝－3(x－40)2＋300，
当x＝40时，P有最大值300，故销售价为40元时，才能获得最大利润.
千里马走向假期期末仿真试卷寒假系列答案
【题目】（本小题12分）根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2．5的年平均浓度不得超过35微克/立方米，PM2．5的24小时平均浓度不得超过75微克/立方米．某城市环保部门随机抽取了一居民区去年20天PM2．5的24小时平均浓度的监测数据，数据统计如下：
]
组别 | PM2.5浓度（微克/立方米） | 频数（天） | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
（Ⅰ）从样本中PM2．5的24小时平均浓度超过50微克/立方米的5天中，随机抽取2天，求恰好有一天PM2．5的24小时平均浓度超过75微克/立方米的概率；
（Ⅱ）求样本平均数，并根据样本估计总体的思想，从PM2．5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由．
