题目内容
【题目】已知函数![]() 为奇函数,且
为奇函数,且![]() 的极小值为
的极小值为![]() .
.![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)求![]() 和
和![]() 的值;
的值;
(2)若关于![]() 的方程
的方程![]() 有三个不等的实数根,求实数
有三个不等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)由![]() 为奇函数可得
为奇函数可得![]() ,然后将
,然后将![]() 代入
代入![]() 中,求出
中,求出![]() 的极小值,根据
的极小值,根据![]() 的极小值为
的极小值为![]() ,可求出
,可求出![]() ,
,![]() 的值;
的值;
(2)构造函数![]() ,将问题转化为
,将问题转化为![]() 与
与![]() 轴有三个交点的问题,根据
轴有三个交点的问题,根据![]() 的单调性可得
的单调性可得![]() ,从而求出
,从而求出![]() 的取值范围.
的取值范围.
解:(1)因为![]() 是奇函数,
是奇函数,
所以![]() 恒成立,
恒成立,
则![]() ,
,
所以![]() ,
,
所以![]() ,
,
则![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
所以![]() 的极小值为
的极小值为![]() ,
,
由![]() ,
,
解得![]() ,
,
所以![]() ,
,![]() ,
,
(2)由(1)可知![]() ,
,![]() ,
,
方程![]() ,
,
即为![]() ,
,
即方程![]() 有三个不等的实数根,
有三个不等的实数根,
设![]() ,只要使曲线有3个零点即可,
,只要使曲线有3个零点即可,
设![]() ,
,
![]() 或
或![]() 分别为
分别为![]() 的极值点,
的极值点,
当![]() 和
和![]() 时,
时,
![]() ,
,![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,
当![]() 时
时![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
所以,![]() 为极大值点,
为极大值点,![]() 为极小值点.
为极小值点.
所以要使曲线与![]() 轴有3个交点,当且仅当
轴有3个交点,当且仅当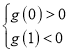 ,
,
即![]() ,
,
解得![]() .
.
即实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
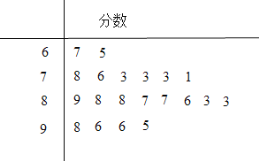
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):若分数不低于95分,则称该员工的成绩为“优秀”.

组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)从这20人中成绩为“优秀”的员工中任取2人,求恰有1人的分数为96的概率;
(Ⅱ)根据这20人的分数补全频率分布表和频率分布直方图,并根据频率分布直方图估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表).