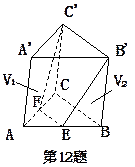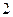题目内容
(本题满分13分)
如图,在六面体 中,平面
中,平面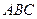 ∥平面
∥平面 ,
,
⊥平面 ,
, ,
,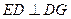 ,
,
 ∥
∥ .且
.且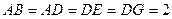 ,
,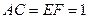 .
.
(1)求证: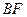 ∥平面
∥平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3) 求五面体 的体积.
的体积.
如图,在六面体
 中,平面
中,平面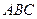 ∥平面
∥平面 ,
,⊥平面
 ,
, ,
,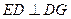 ,
, ∥
∥ .且
.且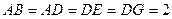 ,
,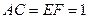 .
.(1)求证:
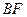 ∥平面
∥平面 ;
;(2)求二面角
 的余弦值;
的余弦值;(3) 求五面体
 的体积.
的体积.(1)略
(2)

(3)4
由已知,AD、DE、DG两两垂直,建立如图的坐标系,

则A(0,0,2),B(2,0,2),C(0,1,2),E(2,0,0),G(0,2,0),F(2,1,0)
(1)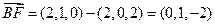 ,
,
∴ ,所以BF∥CG.又BF
,所以BF∥CG.又BF 平面ACGD,故 BF//平面ACGD …4分
平面ACGD,故 BF//平面ACGD …4分
(2)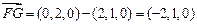 ,设平面BCGF的法向量为
,设平面BCGF的法向量为 ,
,
则 ,令
,令 ,则
,则 ,
,
而平面ADGC的法向量
∴ =
=
故二面角D-CG-F的余弦值为 .9分
.9分
(3)设DG的中点为M,连接AM、FM, 则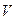 =
=
= =
= =
= .……………13分
.……………13分
解法二设DG的中点为M,连接AM、FM,则由已知条件易证四边形DEFM是平行四边形,
所以MF//DE,且MF=DE又∵AB//DE,且AB=DE ∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,
又BF 平面ACGD 故 BF//平面ACGD……………4分
平面ACGD 故 BF//平面ACGD……………4分
(利用面面平行的性质定理证明,可参照给分)
(Ⅱ)由已知AD⊥面DEFG∴DE⊥AD ,DE⊥DG即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1

∴ , ∴MN=
, ∴MN=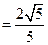 在直角三角形MNF中,MF=2,MN
在直角三角形MNF中,MF=2,MN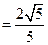
∴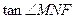 =
= =
= =
= ,
, =
=
故二面角D-CG-F的余弦值为 …………9分
…………9分
(3)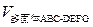 =
= =
=
= =
= .……………13分
.……………13分

则A(0,0,2),B(2,0,2),C(0,1,2),E(2,0,0),G(0,2,0),F(2,1,0)
(1)
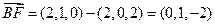 ,
,
∴
 ,所以BF∥CG.又BF
,所以BF∥CG.又BF 平面ACGD,故 BF//平面ACGD …4分
平面ACGD,故 BF//平面ACGD …4分(2)
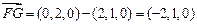 ,设平面BCGF的法向量为
,设平面BCGF的法向量为 ,
,则
 ,令
,令 ,则
,则 ,
,而平面ADGC的法向量

∴
 =
=
故二面角D-CG-F的余弦值为
 .9分
.9分(3)设DG的中点为M,连接AM、FM, 则
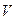 =
=
=
 =
= =
= .……………13分
.……………13分解法二设DG的中点为M,连接AM、FM,则由已知条件易证四边形DEFM是平行四边形,
所以MF//DE,且MF=DE又∵AB//DE,且AB=DE ∴MF//AB,且MF=AB
∴四边形ABMF是平行四边形,即BF//AM,
又BF
 平面ACGD 故 BF//平面ACGD……………4分
平面ACGD 故 BF//平面ACGD……………4分(利用面面平行的性质定理证明,可参照给分)
(Ⅱ)由已知AD⊥面DEFG∴DE⊥AD ,DE⊥DG即DE⊥面ADGC ,
∵MF//DE,且MF=DE , ∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1

∴
 , ∴MN=
, ∴MN=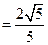 在直角三角形MNF中,MF=2,MN
在直角三角形MNF中,MF=2,MN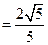
∴
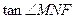 =
= =
= =
= ,
, =
=
故二面角D-CG-F的余弦值为
 …………9分
…………9分(3)
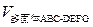 =
= =
=
=
 =
= .……………13分
.……………13分
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
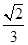
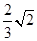
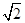
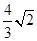

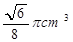


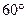 的二面角内放入一个球,球与该二面角的两个半平面分别切于两点A,B,且A、B两点的球面距离为2
的二面角内放入一个球,球与该二面角的两个半平面分别切于两点A,B,且A、B两点的球面距离为2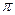 cm,则该球的半径为 .
cm,则该球的半径为 .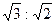
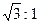

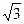
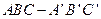
 中,若
中,若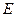 、
、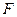 分别为
分别为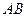 、
、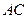 的中点,平面
的中点,平面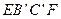 将三棱柱分成体积为
将三棱柱分成体积为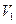 、
、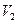 的两部分,那么
的两部分,那么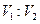 为( )
为( )