题目内容
(本题满分12分)
已知等比数列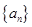 的公比
的公比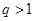 ,
, 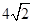 是
是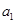 和
和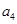 的一个等比中项,
的一个等比中项,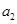 和
和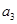 的等差中项为
的等差中项为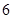 ,若数列
,若数列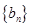 满足
满足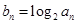 (
(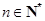 ).
).
(Ⅰ)求数列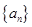 的通项公式; (Ⅱ)求数列
的通项公式; (Ⅱ)求数列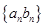 的前
的前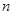 项和
项和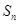 .
.
已知等比数列
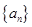 的公比
的公比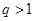 ,
, 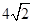 是
是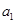 和
和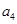 的一个等比中项,
的一个等比中项,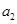 和
和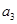 的等差中项为
的等差中项为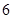 ,若数列
,若数列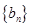 满足
满足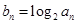 (
(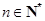 ).
).(Ⅰ)求数列
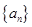 的通项公式; (Ⅱ)求数列
的通项公式; (Ⅱ)求数列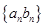 的前
的前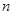 项和
项和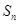 .
.解:(Ⅰ)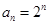 .(Ⅱ)
.(Ⅱ)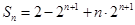
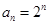 .(Ⅱ)
.(Ⅱ)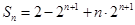
本试题主要是考查了等比数列的通项公式以及数列求和的综合运用。
(1)因为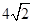 是
是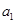 和
和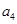 的一个等比中项,,那么利用等比中项可知
的一个等比中项,,那么利用等比中项可知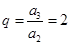 ,,然后得到通项公式。
,,然后得到通项公式。
(2)由于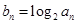 (
(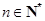 ),所以
),所以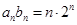 ,利用错位相减法得到结论。
,利用错位相减法得到结论。
解:(Ⅰ)因为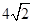 是
是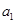 和
和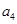 的一个等比中项,
的一个等比中项,
所以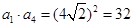 .由题意可得
.由题意可得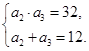 因为
因为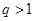 ,所以
,所以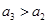 .解得
.解得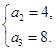
所以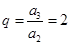 .故数列
.故数列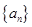 的通项公式
的通项公式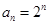 .
.
(Ⅱ)由于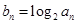 (
(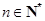 ),所以
),所以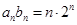 .
.
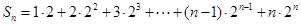 . ①
. ①
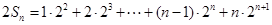 . ②
. ②
①-②得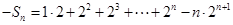
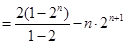 .
.
所以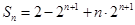
(1)因为
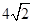 是
是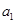 和
和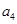 的一个等比中项,,那么利用等比中项可知
的一个等比中项,,那么利用等比中项可知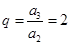 ,,然后得到通项公式。
,,然后得到通项公式。(2)由于
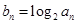 (
(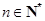 ),所以
),所以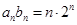 ,利用错位相减法得到结论。
,利用错位相减法得到结论。解:(Ⅰ)因为
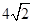 是
是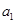 和
和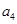 的一个等比中项,
的一个等比中项,所以
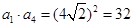 .由题意可得
.由题意可得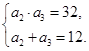 因为
因为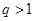 ,所以
,所以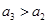 .解得
.解得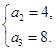
所以
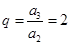 .故数列
.故数列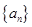 的通项公式
的通项公式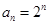 .
.(Ⅱ)由于
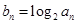 (
(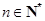 ),所以
),所以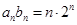 .
.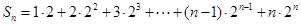 . ①
. ①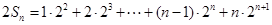 . ②
. ②①-②得
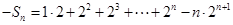
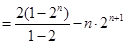 .
.所以
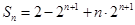

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
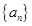 中,
中,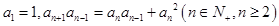 ,
,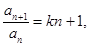
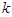
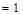 ;(2)求数列
;(2)求数列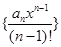 的前
的前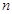 项和。
项和。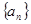 满足
满足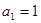 ,
,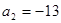 ,
,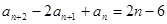
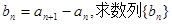 的通项公式;
的通项公式;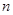 为何值时,
为何值时,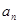 最小(不需要求
最小(不需要求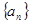 中,
中, 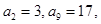 求
求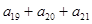 的值。
的值。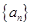 满足
满足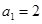 ,
,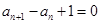
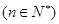 ,则此数列的通项
,则此数列的通项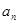 等于( )
等于( )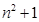
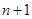
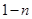
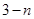
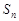 是等差数列
是等差数列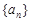 的前
的前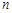 项和,若
项和,若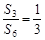 ,则
,则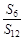 等于( )
等于( )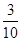
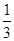
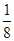
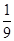
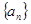 中,
中,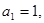 且点
且点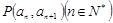 在直线
在直线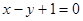 上.
上.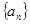 的通项公式;
的通项公式; (2)若函数
(2)若函数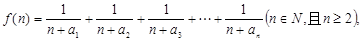 求函数
求函数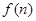 的最小值;
的最小值;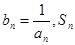 表示数列
表示数列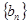 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于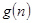 ,使得
,使得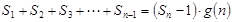 对于一切不小于2的自然数
对于一切不小于2的自然数 的公差是( )
的公差是( )