题目内容
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的离心率为
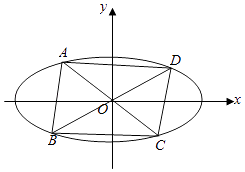
=1(a>b>0)的离心率为 ![]() ,四边形ABCD的各顶点均在椭圆E上,且对角线AC,BD均过坐标原点O,点D(2,1),AC,BD的斜率之积为
,四边形ABCD的各顶点均在椭圆E上,且对角线AC,BD均过坐标原点O,点D(2,1),AC,BD的斜率之积为 ![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过D作直线l平行于AC.若直线l′平行于BD,且与椭圆E交于不同的两点M.N,与直线l交于点P.
⑴证明:直线l与椭圆E有且只有一个公共点;
⑵证明:存在常数λ,使得|PD|2=λ|PM||PN|,并求出λ的值.
【答案】解:(Ⅰ)由题意 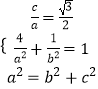 ,解得
,解得 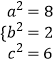 .
.
故椭圆E的方程为 ![]() ;
;
证明:(Ⅱ)(1)由题意 ![]() ,
,
∵ ![]() ,得
,得 ![]() ,则直线l的方程为
,则直线l的方程为 ![]() ,
,
联立 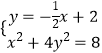 ,化简得x2﹣4x+4=0.
,化简得x2﹣4x+4=0.
∵判别式△=0,∴直线l与椭圆E有且只有一个公共点;
⑵设直线l′的方程为y= ![]() (m≠0).
(m≠0).
联立方程组 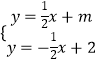 ,解得
,解得 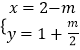 .故点P坐标为(2﹣m,
.故点P坐标为(2﹣m, ![]() ),
), ![]() .
.
联立方程组 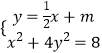 ,化简得x2+2mx+2m2﹣4=0.
,化简得x2+2mx+2m2﹣4=0.
设点M(x1,y1),N(x2,y2).
判别式△=4(﹣m2+4)>0,得﹣2<m<2.
又 ![]() .
.
∴|PM|= ![]() .
.
同理, ![]() .
.
故|PM||PN|= ![]() =
= ![]() =
= ![]() .
.
∵|PD|2=λ|PM||PN|,解得λ=1.
故存在常数λ为1,使得|PD|2=λ|PM||PN|.
【解析】1、(Ⅰ)本题考查的是用待定系数法求椭圆的方程。
(Ⅱ) 由题意 k A C k B D = 1 4 ,∵ ![]() ,得
,得 ![]() ,则直线l的方程为
,则直线l的方程为 ![]() ,
,
联立 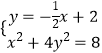 ,化简得x2﹣4x+4=0.∵判别式△=0,∴直线l与椭圆E有且只有一个公共点;
,化简得x2﹣4x+4=0.∵判别式△=0,∴直线l与椭圆E有且只有一个公共点;
2、联立两直线的方程可得故点P坐标为(2﹣m, 1 + ![]() ),
),![]() .再联立直线和椭圆的方程化简得x2+2mx+2m2﹣4=0.
.再联立直线和椭圆的方程化简得x2+2mx+2m2﹣4=0.
设点M(x1,y1),N(x2,y2).判别式△=4(﹣m2+4)>0,得﹣2<m<2.又 ![]() .
.
∴|PM|= ( 2 m x 1) 2 + ( 1 + m 2 y 1) 2 = ![]() | 2 m x 1 |即
| 2 m x 1 |即![]() .故|PM||PN|=
.故|PM||PN|= ![]() .
.
∵|PD|2=λ|PM||PN|,解得λ=1.故存在常数λ为1,使得|PD|2=λ|PM||PN|.