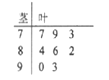
��Ŀ����
����Ŀ��ij�����ij���ǿ��ٳ����������٣�Ϊ�˵��иõ�·�����������ij��ʱ������� ![]() �������ٶȽ���ȡ���������ij����Ƴ���������ͼ��
�������ٶȽ���ȡ���������ij����Ƴ���������ͼ��
�����㣺������ƽ��ֵ ![]() ������
������ ![]() ����Ƶ��ֵ��Ϊ���ʵĹ���ֵ.��֪���ٹ�������춼����Ϊ��������ٶȣ��ֹ涨����С��
����Ƶ��ֵ��Ϊ���ʵĹ���ֵ.��֪���ٹ�������춼����Ϊ��������ٶȣ��ֹ涨����С�� ![]() ���ٴ���
���ٴ��� ![]() ��������ٶ�.
��������ٶ�.
��1���Ӹÿ��ٳ��������г�������ȡ ![]() ������ó�����������ٶȵĸ��ʣ�
������ó�����������ٶȵĸ��ʣ�
��2�� ����������ȡ
����������ȡ ![]() ������������
������������ ![]() ����������������ٶȵĸ���
����������������ٶȵĸ���
��3���Ӹÿ��ٳ��������г�������ȡ ![]() ������������������ٶȵĸ���Ϊ
������������������ٶȵĸ���Ϊ ![]() ����
���� ![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
���𰸡�
��1���⣺���¼� ![]() Ϊ���Ӹÿ��ٳ��������г�������ȡ
Ϊ���Ӹÿ��ٳ��������г�������ȡ ![]() �����ó�����������ٶȡ���
�����ó�����������ٶȡ���
��Ϊ ![]() ��
��
����������ͼ��֪������ĸ���ΪP(A)=![]()
��2���⣺���¼� ![]() Ϊ������������ȡ
Ϊ������������ȡ ![]() ����������
���������� ![]() ����������������ٶȡ�
����������������ٶȡ�
�������֪��������Ϊ ![]() ����������ٶȸ���Ϊ
����������ٶȸ���Ϊ ![]() �������������Ϊ
�������������Ϊ ![]()
��3���⣺������ٶȵĸ��� ![]() ���Ӷ���ֲ�����
���Ӷ���ֲ����� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
![]() ��
��
��� ![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
�� ![]() ��֪��ѧ����
��֪��ѧ���� ![]()
��������(1)������������֪�ɵó� �� 3 �� = 78.4 , �� + 2 �� = 89.4���۲���������ͼ��ͼ��֪P(A)=![]() �����ֵ���ɡ�(2)������֪�������֪��������Ϊ100����������ٶȸ���Ϊ 5 �����ݸ��ʵĶ��������ֵ��(3)���ն���ֲ��Ĺ�ʽ
�����ֵ���ɡ�(2)������֪�������֪��������Ϊ100����������ٶȸ���Ϊ 5 �����ݸ��ʵĶ��������ֵ��(3)���ն���ֲ��Ĺ�ʽ![]() ��һ������ֵ���������б����ɣ��ٽ����ѧ����
��һ������ֵ���������б����ɣ��ٽ����ѧ����![]() �Ĺ�ʽ������ֵ������ɡ�
�Ĺ�ʽ������ֵ������ɡ�
�����㾫����ͨ�����������������Ƶ�ʷֲ���������ֲ��������������ݵ�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ����ͨ����С��������������������ռ������С����ʾ���ݵķֲ����ɣ������������Ǹ�����Ŀ��������������ݵ�Ƶ�ʷֲ���������ɴ˹�������ķֲ���������Խ����⣮