题目内容
19.已知数列{an},a1=1,an+1=$\frac{{a}_{n}}{1+2{a}_{n}}$(n=1,2,3,…).(1)求a2、a3、a4;
(2)归纳猜想通项公式an,并用数学归纳法证明.
分析 (1)由a1=1,an+1=$\frac{{a}_{n}}{1+2{a}_{n}}$(n=1,2,3,…),分别令n=1,2,3,即可得出;
(2)由(1)猜想:an=$\frac{1}{2n-1}$.利用数学归纳法证明即可.
解答 解:(1)∵a1=1,an+1=$\frac{{a}_{n}}{1+2{a}_{n}}$(n=1,2,3,…).∴a2=$\frac{{a}_{1}}{1+2{a}_{1}}$=$\frac{1}{3}$,同理可得:a3=$\frac{1}{5}$,a4=$\frac{1}{7}$.
(2)由(1)猜想:an=$\frac{1}{2n-1}$.
下面利用数学归纳法证明:
①当n=1时,成立;
②假设当n=k时,ak=$\frac{1}{2k-1}$.
则当n=k+1(k∈N*)时,ak+1=$\frac{{a}_{k}}{1+2{a}_{k}}$=$\frac{\frac{1}{2k-1}}{1+\frac{2}{2k-1}}$=$\frac{1}{2k+1}$=$\frac{1}{2(k+1)-1}$,
因此当n=k+1时,命题成立.
综上①②可知:?n∈N*,an=$\frac{1}{2n-1}$都成立.
点评 本题考查了数学归纳法、递推公式、数列的通项公式,考查了猜想归纳能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.下列函数与函数y=x是相同的函数是( )
| A. | y=$\frac{{x}^{2}}{x}$ | B. | y=($\sqrt{x}$)2 | C. | y=($\root{3}{x}$)3 | D. | y=|x| |
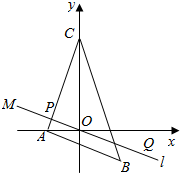 如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.
如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.