题目内容
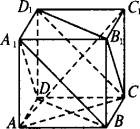
如图，在棱长为a的正方体中．(1)求证：平面A1BD∥平面CB1D1；
(2)作出两平行平面的公垂线．
答案：D
解析：
解析：
(1)证明：由正方体ABCD—A1B1C1D1知，A1B1 AB，AB CD，∴A1B1 CD．
∴四边形A1B1CD为平行四边形．∴A1D∥B1C． 而B1C 同理BD∥平面CB1D1，且A1D∩BD=D． ∴平面A1BD∥平面CB1D1． (2)连结AC1、AC，由正方体的性质知 C1C⊥CD，C1C⊥BC，AC⊥BD． ∴C1C⊥面AC．∴AC1⊥BD． 同理AC1⊥A1B．∴AC1⊥平面A1BD． 同理AC1⊥平面CB1D1， 即AC1是平面A1BD和平面CB1D1的公垂线．
|
练习册系列答案
相关题目
如图，在棱长为2的正四面体A-BCD中，若以△ABC为视角正面，则其正视图的面积是（ ）
，当
取什么位置时，三棱柱的体积最大？
，AG＝
，给出下列四个命题：①AC⊥BD，②FG＝
，③侧面与底面所成二面角的余弦值为
，④
，其中真命题的序号是（ ）
