题目内容
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,上顶点为B,O为坐标原点,且向量
,上顶点为B,O为坐标原点,且向量![]() 与
与![]() 的夹角为
的夹角为![]() .
.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 设
设![]() ,点P是椭圆
,点P是椭圆![]() 上的动点,求
上的动点,求![]() 的最大值和最小值;
的最大值和最小值;
![]() 设不经过点B的直线l与椭圆
设不经过点B的直线l与椭圆![]() 相交于M、N两点,且直线BM、BN的斜率之和为1,证明:直线l过定点.
相交于M、N两点,且直线BM、BN的斜率之和为1,证明:直线l过定点.
【答案】(1)![]() ;(2)最大值6,最小
;(2)最大值6,最小![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由向量![]() 与
与![]() 的夹角为
的夹角为![]() ,可得
,可得![]() 可得
可得![]() ,即可得到椭圆方程;(2)设
,即可得到椭圆方程;(2)设![]() ,代入椭圆方程,结合数量积公式可得
,代入椭圆方程,结合数量积公式可得![]() ,利用二次函数的性质可得结果;(3)设不经过点
,利用二次函数的性质可得结果;(3)设不经过点![]() 的直线
的直线![]() 方程为:
方程为:![]() ,联立椭圆方程可得
,联立椭圆方程可得![]() ,运用韦达定理和直线的斜率公式,化简
,运用韦达定理和直线的斜率公式,化简![]() 可得
可得![]() ,代入直线方程即可得证.
,代入直线方程即可得证.
![]() 椭圆
椭圆![]() :
:![]() 的
的![]() ,向量
,向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
可得![]() ,即
,即![]() ,
,
则椭圆方程为![]() ;
;
![]() 设
设![]() ,可得
,可得![]() ,即
,即![]() ,
,
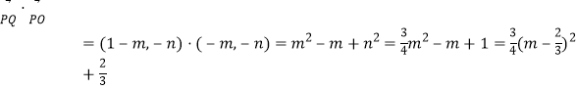 ,
,
由![]() 可得
可得![]() 时,上式取得最小值
时,上式取得最小值![]() ;
;![]() 时,取得最大值6,
时,取得最大值6,
则![]() 的范围是
的范围是![]() ;
;
![]() 证明:当直线l的斜率不存在时,设
证明:当直线l的斜率不存在时,设![]() ,
,![]() ,
,
由![]() ,
,
![]() ,
,![]() ,得
,得![]() ,此时M,N重合,不符合题意;
,此时M,N重合,不符合题意;
设不经过点P的直线l方程为:![]() ,
,![]() ,
,![]() ,
,
由![]() 得
得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
直线l必过定点![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目

