题目内容
【题目】如图,已知中心在原点,焦点在![]() 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为![]() ,
,![]() 是椭圆上一点.
是椭圆上一点.
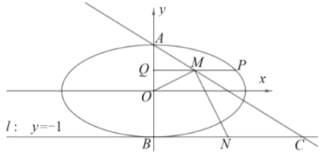
(1)求椭圆的标准方程;
(2)设椭圆的上下顶点分别为![]() ,
,![]() ,
,![]() 是椭圆上异于
是椭圆上异于![]()
![]() 的任意一点,
的任意一点,![]() 轴,
轴,![]() 为垂足,
为垂足,![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
①求证:![]() ;
;
②若![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
【答案】(1)![]() (2)①证明见解析;②
(2)①证明见解析;②![]()
【解析】
(1)设椭圆方程为![]() ,由题意,得
,由题意,得![]() ,再由
,再由![]() 是椭圆上的一个点,即可求出椭圆方程;
是椭圆上的一个点,即可求出椭圆方程;
(2)根据题意,求出直线AB的方程、点M,C,N的坐标,计算![]() ,可得
,可得![]() ,再利用
,再利用![]() ,结合椭圆方程,求解可得结果.
,结合椭圆方程,求解可得结果.
(1)设椭圆方程为![]() ,
,
由题意,得![]() .因为
.因为![]() ,所以
,所以![]() .
.
又![]() 是椭圆上的一个点,所以
是椭圆上的一个点,所以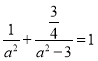 ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以椭圆的标准方程为![]() .
.
(2)①解:因为![]() ,
,![]() ,则
,则![]() ,且
,且![]() .
.
因为![]() 为线段
为线段![]() 中点,所以
中点,所以![]() .
.
又![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
因为![]() ,∴
,∴![]()
令![]() ,得
,得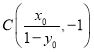 ,
,
又![]() ,
,![]() 为线段
为线段![]() 的中点,有
的中点,有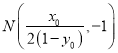 ,
,
所以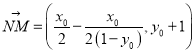 .
.
因此,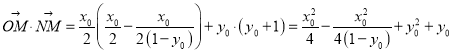
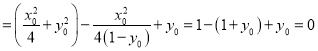 .
.
所以![]() .
.
②由①知,![]() .
.
因为![]() ,
,
所以在![]() 中,
中,![]() ,
,
因此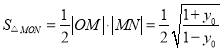 ,从而有
,从而有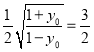 ,
,
解得![]() .
.

练习册系列答案
相关题目