题目内容
6.已知f(x)=$\left\{\begin{array}{l}{3|lo{g}_{3}x|,0<x≤3}\\{(x-4)(x-6),x>3}\end{array}\right.$,若f(a)=f(b)=f(c)=f(d),且a<b<c<d,则abcd的取值范围是( )| A. | (23,24) | B. | (24,27) | C. | (21,24) | D. | (24,25) |
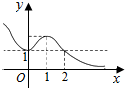
分析 图象法:画出函数y=f(x)的图象,根据图象分析a,b,c,d的关系及取值范围,从而求出abcd的取值范围
解答 解:先画出f(x)=$\left\{\begin{array}{l}{3|lo{g}_{3}x|,0<x≤3}\\{(x-4)(x-6),x>3}\end{array}\right.$的图象,如图:
∵a,b,c,d互不相同,不妨设a<b<c<d.
且f(a)=f(b)=f(c)=f(d),3<c<4,d>6.
∴-log3a=log3b,c+d=10,
即ab=1,c+d=10,
故abcd=c(10-c)=-c2+10c,由图象可知:3<c<4,
由二次函数的知识可知:-32+10×3<-c2+10c<-42+10×4,
即21<-c2+12c<24,
∴abcd的范围为(21,24).
故选:C.
点评 本题考查了利用函数图象分析解决问题的能力,以及对数函数图象的特点,注意体会数形结合思想在本题中的运用

练习册系列答案
相关题目
15.下列四个选项表示的集合中,有一个集合不同于另三个集合,这个集合是( )
| A. | {x|x=0} | B. | {a|a2=0} | C. | {a=0} | D. | {0} |
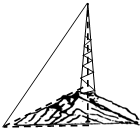 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30米,在地面上 已知抛物线y2=2px(p>0),点E(2,1),若斜率为2的弦过点E,且以E为弦中点.
已知抛物线y2=2px(p>0),点E(2,1),若斜率为2的弦过点E,且以E为弦中点.