题目内容
14.已知:函数y=f(x)是周期为4的奇函数,且当x∈[0,1]时,y=log2x,求当x∈[3,4]时,函数的解析式.分析 先设x∈[-1,0],运用取相反数和奇函数的定义,转化为[0,1],利用周期性和符号把“x-4”转化到区间[-1,0],代入函数解析式,再利用周期性,求出f(x)在[3,4]上的解析式.
解答 解:设x∈[-1,0],则-x∈[0,1],
∵当x∈[0,1]时,f(x)=log2x,
∴f(-x)=log2(-x),
由f(x)为奇函数,即有f(-x)=-f(x),
则f(x)=-log2(-x),x∈[-1,0],
由函数y=f(x)是周期为4的函数,
令x∈[3,4],则x-4∈[-1,0],
即有f(x-4)=-log2(4-x),
则有f(x)=f(x-4)=-log2(4-x),x∈[3,4].
点评 本题考查了求定区间上的函数解析式,一般的做法是“求谁设谁”,即在那个区间上求解析式,x就设在该区间内,再利用函数的周期和负号转化到已知的区间上,代入解析式进行化简,再利用奇函数的定义和周期性求出f(x).

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
4.若函数f(x)=$\frac{ax+1}{x+2}$在(-2,2)内为增函数,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,+∞) | B. | [$\frac{1}{2}$,+∞) | C. | (-∞,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$] |
5.如图给出的是计算和式$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )
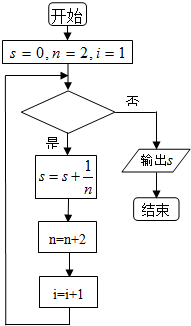

| A. | i≤11 | B. | i≤10 | C. | i≥10 | D. | i≥11 |
9.命题“若p3+q3=2,则p+q≤2”的结论的否定应该是( )
| A. | p+q=2 | B. | p+q≥2 | C. | p+q≠2 | D. | p+q>2 |
6.已知f(x)=$\left\{\begin{array}{l}{3|lo{g}_{3}x|,0<x≤3}\\{(x-4)(x-6),x>3}\end{array}\right.$,若f(a)=f(b)=f(c)=f(d),且a<b<c<d,则abcd的取值范围是( )
| A. | (23,24) | B. | (24,27) | C. | (21,24) | D. | (24,25) |
3.若变量x,y满足约束条件:$\left\{{\begin{array}{l}{0≤x≤7}\\{2≤y≤8}\\{3x-y≥1}\end{array}}\right.$,则变量z=x-y的取值情况是( )
| A. | 既没有最大值也没有最小值 | B. | 有最大值5,没有最小值 | ||
| C. | 有最小值-1,没有最大值 | D. | 有最小值-5,也有最大值5 |
4.圆x2+y2+2x-4y-4=0的圆心坐标和半径分别是( )
| A. | (-1,2),3 | B. | (-1,2),9 | C. | (1,-2),3 | D. | (1,-2),9 |