题目内容
8.直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=1,直线B1C与平面ABC成30°,求点B到平面AC1的距离及二面角B-CC1-A的大小.分析 通过已知条件已知AB=1即为点B到平面AC1的距离,利用直线B1C与平面ABC成30°可求得BC,解Rt△ABC即可.
解答 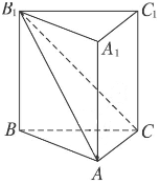 解:∵∠BAC=90°,三棱柱ABC-A1B1C1为直三棱柱,
解:∵∠BAC=90°,三棱柱ABC-A1B1C1为直三棱柱,
∴AB=1即为点B到平面AC1的距离,
∠ACB即为二面角B-CC1-A的平面角,
∵AB=BB1=1,直线B1C与平面ABC成30°,
∴∠BCB1=30°,
∴BC=BB1•cot30°=$\sqrt{3}$,
∴sin∠ACB=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,
∴∠ACB=arcsin$\frac{\sqrt{3}}{3}$.
点评 本题考查线面角、二面角,考查解三角形,注意解题方法的积累,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.若实数a,b,c,d满足(b+a2-3lna)2+(c-d+2)2=0,则(a-c)2+(b-d)2的最小值为( )
| A. | $\sqrt{2}$ | B. | 8 | C. | $2\sqrt{2}$ | D. | 2 |