题目内容
【题目】椭圆![]() 的右顶点为
的右顶点为![]() ,左焦点为
,左焦点为![]() ,离心率为
,离心率为![]() ,已知
,已知![]() 也是抛物线
也是抛物线![]() 的焦点,
的焦点, ![]() 到准线的距离为
到准线的距离为![]()
(1)求椭圆的方程和抛物线的方程;
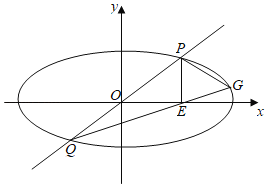
(2)过原点的直线交![]() 于
于![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于另一点
于另一点![]() .
.
①证明:![]() 三点共线
三点共线
②求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;
;![]() ;(2)证明见详解(3)
;(2)证明见详解(3)![]()
【解析】
(1)分析条件可知,![]() ,
,![]() ,再结合椭圆关系式
,再结合椭圆关系式![]() 即可求解,又
即可求解,又![]() ,
,![]() 也可求解
也可求解
(2)可采用点差法,设![]() ,
,![]() ,则
,则![]() ,设直线
,设直线![]() ,利用
,利用![]() (利用点差法证明)可求
(利用点差法证明)可求![]() ,再表示出
,再表示出![]() ,只需证明
,只需证明![]() 即可
即可
(3)利用![]() ,代入已得数据,并对
,代入已得数据,并对![]() 换元,利用“对勾”函数可得最值
换元,利用“对勾”函数可得最值
(1)由题可知:![]() ,
,![]() ,又椭圆有
,又椭圆有![]() ,联立求解可得
,联立求解可得![]() ,故椭圆的标准方程为:
,故椭圆的标准方程为:![]() ;
;
又![]() ,故抛物线的方程为:
,故抛物线的方程为:![]() ;
;
(2)
①设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,设直线
,设直线![]() ,
,
则![]() ,
,![]() ,
,
![]()
![]() 在椭圆上,
在椭圆上,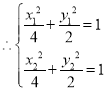 ,联立求解变形可得
,联立求解变形可得![]() ,
,
即![]() ,则
,则![]() ,
,
![]() ,
,![]() ,故
,故![]() 三点共线;
三点共线;
②
设直线![]() 的方程为:
的方程为:![]() ,
,
与![]() 联立消去
联立消去![]() ,
,
得![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
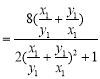
令![]() ,则
,则![]() ,
,
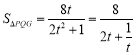
利用“对勾”函数![]() 在
在![]() ,
,![]() 的单调性可知,
的单调性可知,
![]() 时取等号),
时取等号),
![]()
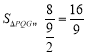 (此时
(此时![]() ,
,
故![]() 面积的最大值为
面积的最大值为![]() .
.

【题目】为方便市民出行,倡导低碳出行.某市公交公司推出利用支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,在推广期内采用随机优惠鼓励市民扫码支付乘车.该公司某线路公交车队统计了活动推广期第一周内使用扫码支付的情况,其中![]() (单位:天)表示活动推出的天次,
(单位:天)表示活动推出的天次,![]() (单位:十人次)表示当天使用扫码支付的人次,整理后得到如图所示的统计表1和散点图.
(单位:十人次)表示当天使用扫码支付的人次,整理后得到如图所示的统计表1和散点图.
表1:
x | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 |
y | 7 | 12 | 20 | 33 | 54 | 90 | 148 |

(1)由散点图分析后,可用![]() 作为该线路公交车在活动推广期使用扫码支付的人次
作为该线路公交车在活动推广期使用扫码支付的人次![]() 关于活动推出天次
关于活动推出天次![]() 的回归方程,根据表2的数据,求此回归方程,并预报第8天使用扫码支付的人次(精确到整数).
的回归方程,根据表2的数据,求此回归方程,并预报第8天使用扫码支付的人次(精确到整数).
表2:
|
|
| img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/08/08/88254471/SYS201908080801220877999013_ST/SYS201908080801220877999013_ST.008.png" width="67" height="40" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> |
|
|
4 | 52 | 3.5 | 140 | 2069 | 112 |
表中![]() ,
,![]() .
.
(2)推广期结束后,该车队对此期间乘客的支付情况进行统计,结果如表3.
表3:
支付方式 | 现金 | 乘车卡 | 扫码 |
频率 | 10% | 60% | 30% |
优惠方式 | 无优惠 | 按7折支付 | 随机优惠(见下面统计结果) |
统计结果显示,扫码支付中享受5折支付的频率为![]() ,享受7折支付的频率为
,享受7折支付的频率为![]() ,享受9折支付的频率为
,享受9折支付的频率为![]() .已知该线路公交车票价为1元,将上述频率作为相应事件发生的概率,记随机变量
.已知该线路公交车票价为1元,将上述频率作为相应事件发生的概率,记随机变量![]() 为在活动期间该线路公交车搭载乘客一次的收入(单位:元),求
为在活动期间该线路公交车搭载乘客一次的收入(单位:元),求![]() 的分布列和期望.
的分布列和期望.
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为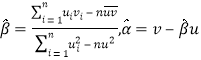 参考数据:
参考数据:![]() ,
,![]() ,
,![]() .
.