题目内容
【题目】如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱![]() 。
。

(1)证明FO∥平面CDE;
(2)设BC=![]() CD,证明EO⊥平面CDE。
CD,证明EO⊥平面CDE。
【答案】(1)证明见解析;(2) 证明见解析;
【解析】
(1)利用中点做辅助线,构造出平行四边形即可证明线面平行;(2)根据所给条件构造出菱形,再根据两个对应的线段垂直关系即可得到线面垂直.
证明:(1)取CD中点M,连结OM,连结EM,
在矩形ABCD中,![]() 又
又![]() ,
,
则![]() ,于是四边形EFOM为平行四边形。
,于是四边形EFOM为平行四边形。
∴FO∥EM.
又∵FO![]() 平面CDE,且EM
平面CDE,且EM![]() 平面CDE,
平面CDE,
∴FO∥平面CDE。
(2)连结FM,
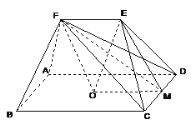
由(1)和已知条件,在等边ΔCDE中,CM=DM,EM⊥CD
且![]()
因此平行四边形EFOM为菱形,从而EO⊥FM.
∵CD⊥OM,CD⊥EM
∴CD⊥平面EOM,
从而CD⊥EO.
而FM![]() CD=M,所以EO⊥平面CDF.
CD=M,所以EO⊥平面CDF.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
【题目】某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价![]() 元与日销售量
元与日销售量![]() 件之间有如下关系:
件之间有如下关系:
x | 45 | 50 |
y | 27 | 12 |
(1)确定![]() 与
与![]() 的一个一次函数关系式
的一个一次函数关系式![]() ;
;
(2)若日销售利润为P元,根据(I)中关系写出P关于![]() 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?