题目内容
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() .点
.点![]() 是
是![]() 上的定点,
上的定点,![]() ,
,![]() 是
是![]() 上的两动点,且线段
上的两动点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
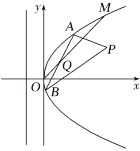
(Ⅰ)求曲线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)记![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ,
,![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)由抛物线准线方程及P到准线的距离,可求得![]() ,进而求得抛物线方程,将点M的坐标代入抛物线 ,即可求得t.
,进而求得抛物线方程,将点M的坐标代入抛物线 ,即可求得t.
(Ⅱ)求直线OM方程,点Q在直线OM上,根据直线方程表示点Q坐标,消去参数n,
利用点差法表示出直线AB斜率,进而求出直线方程,将直线AB方程与抛物线方程联立,用弦长公式求弦长,从而将d表示为关于m的函数,根据m范围求最值.
详解:(1)![]() 的准线为
的准线为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴抛物线![]() 的方程为
的方程为![]() .又点
.又点![]() 在曲线
在曲线![]() 上,∴
上,∴![]() .
.
(2)由(1)知,点![]() ,从而
,从而![]() ,即点
,即点![]() ,
,
依题意,直线![]() 的斜率存在,且不为
的斜率存在,且不为![]() ,
,
设直线![]() 的斜率为
的斜率为![]() .且
.且![]() ,
,![]() ,
,
由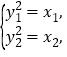 得
得![]() ,故
,故![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由![]() 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
从而![]() .
.
∴![]() ,
,
当且仅当![]() ,即
,即![]() 时,上式等号成立,
时,上式等号成立,
又![]() 满足
满足![]() .∴
.∴![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目

