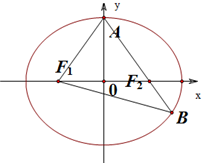
题目内容

已知F1，F2是椭圆
x2
k+2
+
y2
k+1
=1的左、右焦点，过F1的直线交椭圆于A，B两点，若△ABF2的周长为8，则k的值为______．
∵方程
x2
k+2
+
y2
k+1
=1表示焦点在x轴上的椭圆，
∴k+2＞k+1＞0，可得k＞-1．
因此a2=k+2，解得a=
k+2
．
根据椭圆的定义，得|AF1|+|AF2|=|BF1|+|BF2|=2a，
∴|AF1|+|BF1|+|AF2|+|BF2|=4a．
∵线段AB经过左焦点F1，△ABF2的周长为8，
∴|AB|+|AF2|+|BF2|=8，即|AF1|+|BF1|+|AF2|+|BF2|=4a=8，
解得a=
k+2
=2，可得k=2．
故答案为：2
练习册系列答案
相关题目
已知椭圆
x2
16
+
y2
9
=1的左、右焦点分别为F1、F2，P是椭圆上的一点，Q是PF1的中点，若|OQ|=1，则|PF1|=______．
如图，F1、F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2=60°．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）已知△AF1B的面积为40
3
，求a，b的值．
椭圆x2+4y2=4的焦距为（　　）
A．2B．3C．2
3
D．4
过椭圆左焦点F且倾斜角为60°的直线交椭圆于A，B两点，若|FA|=
3
2
|FB|，则椭圆的离心率等于（　　）
A．
2
3
B．
2
5
C．
1
2
D．
2
3
点P在椭圆
x2
4
+
y2
3
=1上运动，Q、R分别在两圆（x+1）2+y2=1和（x-1）2+y2=1上运动，则|PQ|+|PR|的最小值为______．
已知椭圆
x2
20
+
y2
k
=1的焦距为6，则k的值为（　　）
A．13或27B．11或29C．15或28D．10或26
若直线mx+y+n-1=0（mn＞0）经过椭圆
x2
4
+
y2
3
=1的右焦点，则
1
m
+
1
n
的最小值为______．
“神舟”五号飞船的运行轨道是以地心为一个焦点的椭圆，地球半径为R公里，飞船的近地点（距离地球最近的点）距地球地面200公里，远地点（距离地球最远的点）距地面地面350公里，则飞船轨道的离心率为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网