题目内容
【题目】已知数列{an}是首项为a1= 
，公比q= 的等比数列，设bn+2=3 
an（n∈N*），数列{cn}满足cn=anbn ．
（1）求证：{bn}是等差数列；
（2）求数列{cn}的前n项和Sn；
（3）若cn≤ m2+m﹣1对一切正整数n恒成立，求实数m的取值范围．
【答案】
（1）证明：由题意得，an= 
= 
，
又bn+2=3 
an（n∈N*），则bn+2=3 =3n，
所以bn=3n﹣2，即bn+1﹣bn=3，且b1=1，
所以{bn}是为1为首项，3为公差的等差数列
（2）证明：解：由（1）得，an= ，bn=3n﹣2
所以cn=anbn= 
，
则Sn= 
①，
Sn= 
②，
① ﹣②得， 
Sn= 
= 
= 
，
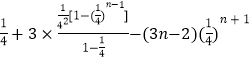
所以Sn= 
（3）证明：由（2）得，cn= ，
cn+1﹣cn= 
﹣ = 
，
所以当n=1时，c2=c1= ，
当n≥2时，c2=c1＞c3＞c4＞c5＞…＞cn，
则当n=1或2时，cn的最大值是 ，
因为cn≤ 
m2+m﹣1对一切正整数n恒成立，
所以 ≤ m2+m﹣1，即m2+4m﹣5≥0，解得m≥1或m≤﹣5，
故实数m的取值范围是m≥1或m≤﹣5
【解析】（1）根据题意和等比数列的通项公式求出an ， 再由对数的运算性质求出bn ， 根据等差数列的定义进行证明；（2）由（1）和题意求出数列{cn}的通项公式，利用错位相减法能求出数列{cn}的前n项和；（3）先化简cn+1﹣cn ， 再根据结果的符号与n的关系，判断出数列{cn}的最大项，将恒成立问题转化为具体的不等式，再求出实数m的取值范围．
【考点精析】根据题目的已知条件，利用数列的前n项和的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系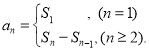
．
