Question

【题目】从某企业生产的某中产品中抽取100件，测量这些产品的质量指标值．由测量结果得到如图所示的频率分布直方图，质量指标值落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．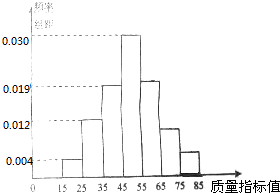

（1）求这些产品质量指标落在区间[75，85]内的概率；
（2）用分层抽样的方法在区间[45，75）内抽取一个容量为6的样本，将该样本看成一个总体，从中任意抽取2件产品，求这2件产品都在区间[45，65）内的概率．

Answer 1

【答案】
（1）解：由题意，质量指标值落在区间[55，65），[65，75），[75，85]内的频率之和为1﹣0.04﹣0.12﹣0.19﹣0.3=0.35，

∵质量指标值落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1，

∴这些产品质量指标值落在区间[75，85]内的频率为0.35× =0.05，

（2）解：由频率分布直方图得：这些产品质量指标值落在区间[55，65）内的频率为0.35× =0.2，

这些产品质量指标值落在区间[65，75）内的频率为0.35× =0.1，

这些产品质量指标值落在区间[45，55）内的频率为0.03×10=0.30，

所以这些产品质量指标值落在区间[45，65）内的频率为0.3+0.2=0.5，

∵ =

∴从[45，65）的产品数中抽取6× =5件，记为A，B，C，D，E，从[65，75）的产品数中抽取6× =1件，记为a，

从中任取两件，所有可能的取法有：（A，B），（A，C），（A，D），（A，E），（A，a），（B，C），（B，D），（B，E），（B，a），（C，D），（D（C，E），（C，a），（D，E），（D，a），（E，a），共15种，

这2件产品都在区间[45，65）内的取法有10种，

∴从中任意抽取2件产品，求这2件产品都在区间[45，65）内的概率 = ．

【解析】（1）由题意，质量指标值落在区间[55，65），[65，75），[75，85]内的频率之和，利用之比为4：2：1，即可求出这些产品质量指标值落在区间[75，85]内的频率；（2）由频率分布直方图得从[45，65）的产品数中抽取5件，记为A，B，C，D，E，从[65，75）的产品数中抽取1件，记为a，由此利用列举法求出概率．
【考点精析】认真审题，首先需要了解频率分布直方图(频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息)．